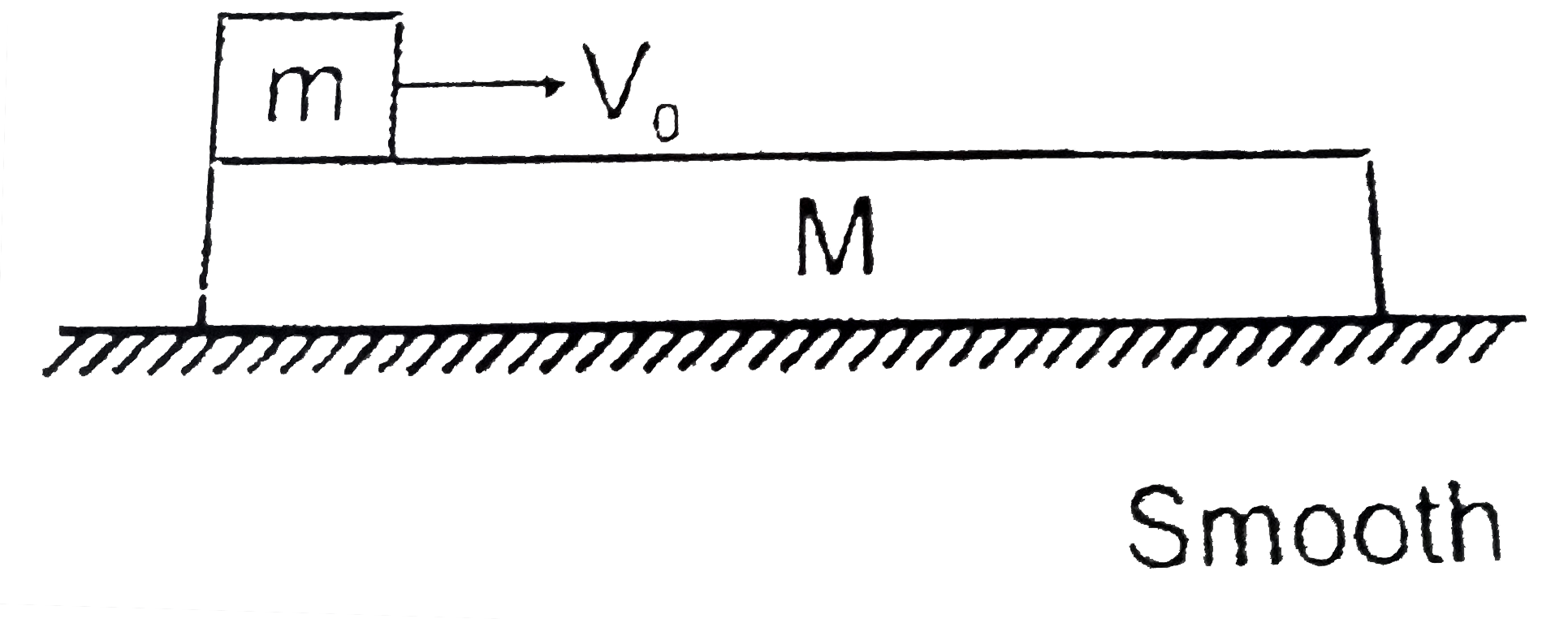
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
the work done by friction on the blcok is negative
the work done by friction on the plank is positive
the net work done by friction is negative
net work done by the friction is zero
NA
Topper's Solved these Questions
Similar Questions
A plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?
View SolutionIn the adjoining figure, the coefficient of friction between wedge ( of mass M) and block ( of mass m) is μ.
Find the minimum horizontal force F rquired to keep the block stationary with respect to wedge

View Solution
Knowledge Check
A block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
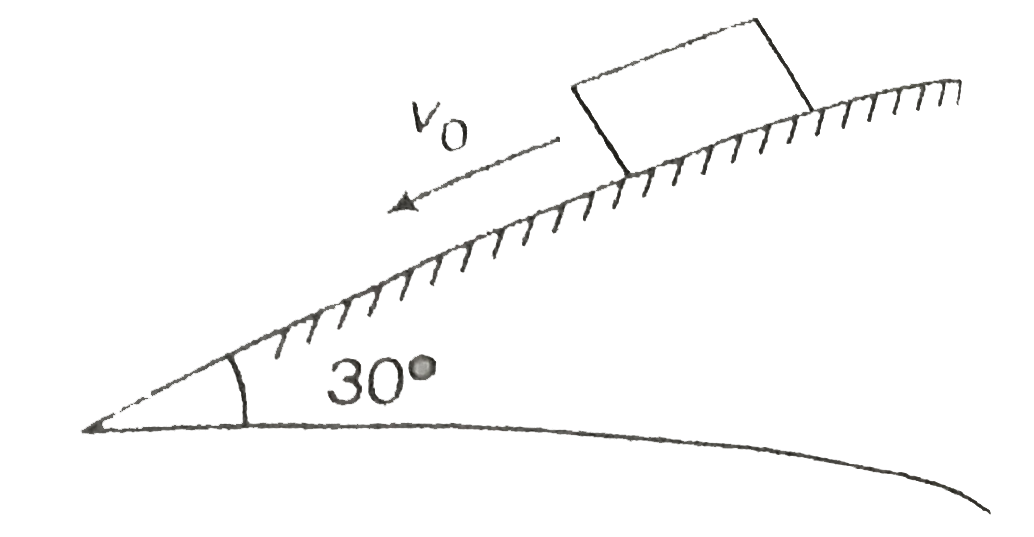 Acontinue of move down the plane with constant velocity v0Baccelerate downwardCdecelerate and come to restDfirst accelerate downward then decelerate
Acontinue of move down the plane with constant velocity v0Baccelerate downwardCdecelerate and come to restDfirst accelerate downward then decelerateThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between A&B is released from rest & there is no slipping between A&B then:
 A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)A block of mass m is placed gently onto a long plank of mass M moving with a velocity v0 on a smooth horizontal floor. If friction is present between M and m :
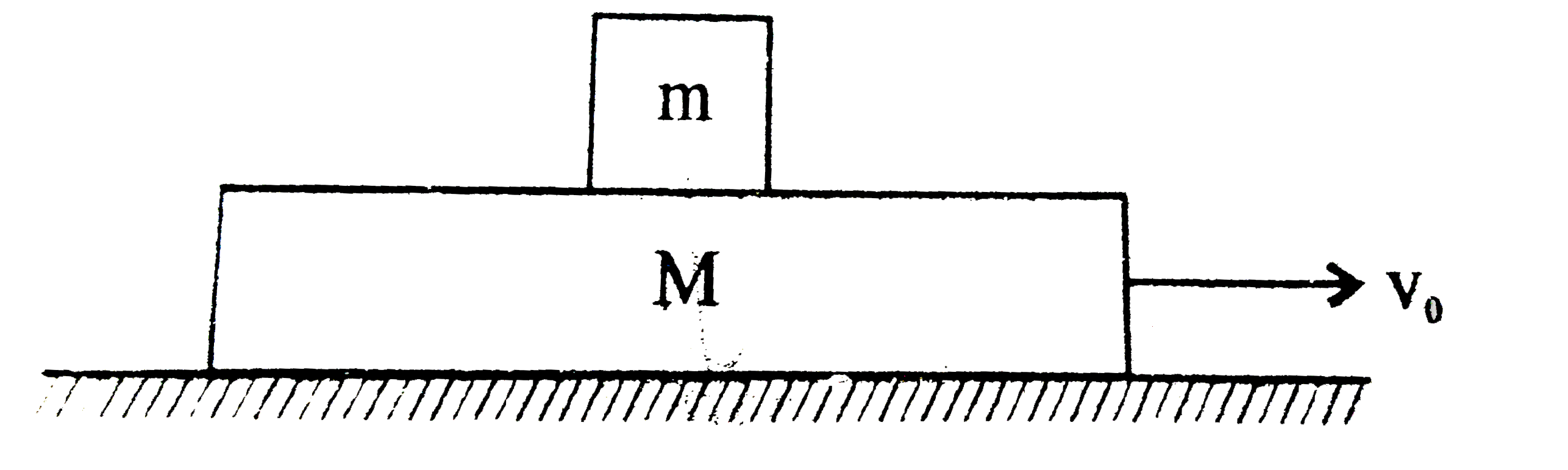 Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
The block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block
View SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface A small block of mass m is projected wii:h a velocity v0 as shown in the Fig. 3.31 (a), The coefficient of friction between the block and the plank is μ, plank is very long so that block eventually comes to rest on it.
(i) Find the work done by the ftjctioh force on the block during the period it slides on the plank. Is the Work positive or negative ?'
(ii) Calculate the work done on the plank during the same period. Is the work positive or negative?
(iii) Also, determine the net work done by friction. Is it positive or negative ?

View SolutionIn the adjoining figure, the coefficient of friction between wedge (of mass M) and block (of mass m) is μ.
Find the minimum horizontal force F required to keep the block stationary with respect to wedge.

View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View Solution
