In the previous question, in place of disc a ring is used whose inner radius is R1 and outer radius is R2 Now how much extra weight should be added on the other side, so that the ring can just come out of water ?
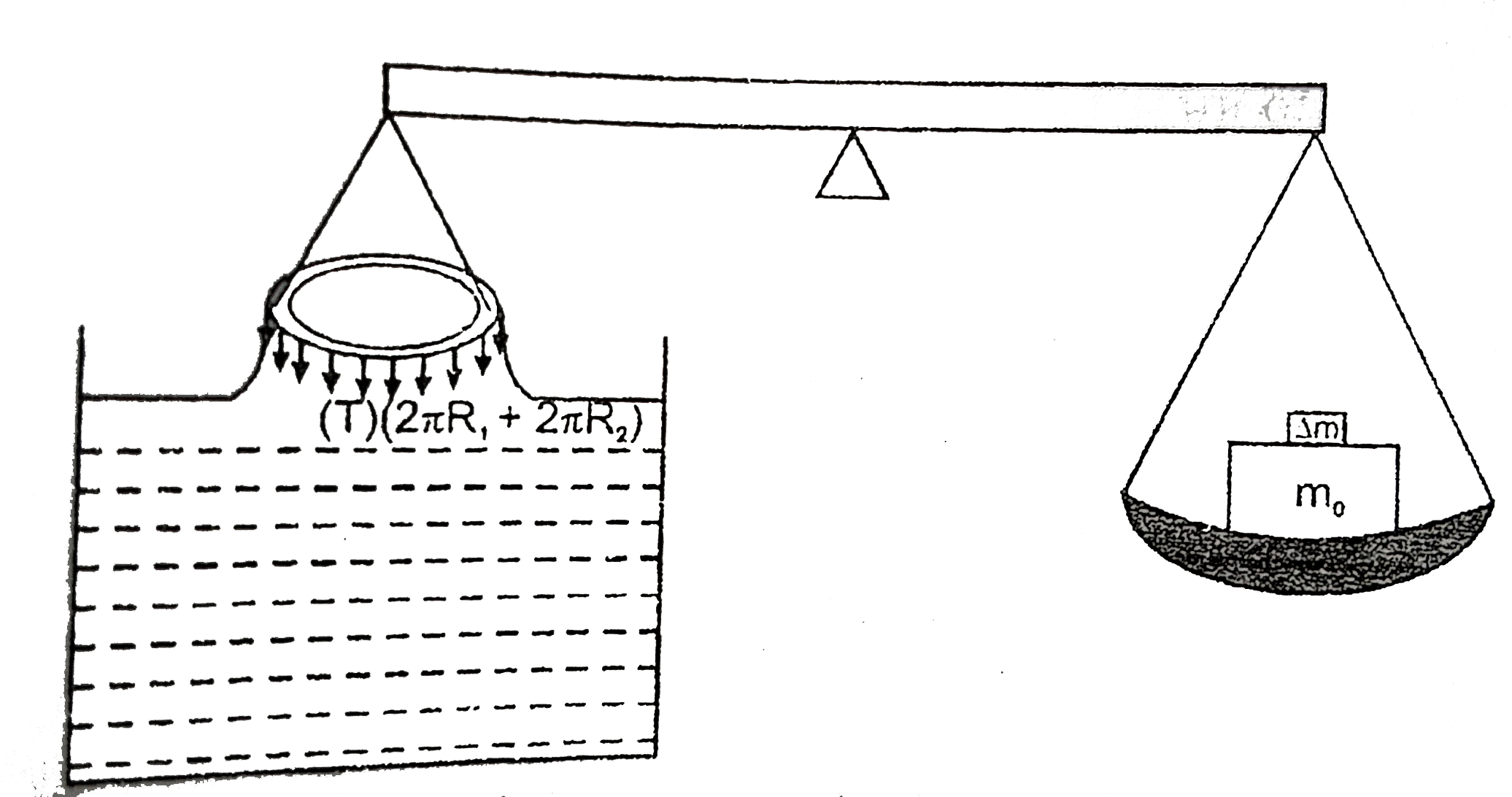
Surface tension force on the disc is (T)2π(R1+R2)
For balance (T)2π(R1+R2)=(Δm)g⇒(T)2π(R1)−R2g
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I10videos
SURFACE TENSION
- BOOK - RESONANCECHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II17videos
SURFACE TENSION
- BOOK - RESONANCECHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
- BOOK - RESONANCECHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise27videos
UNITS, DIMENSION & MEASUREMENT
Similar Questions
A thin disc of radius R, just touching the liquid surface forms one arm of a balance. The palte is balanced by some weight on the other side of the balance. How much extra weight should be added on the other side, so that the disc can just come cut of water ?
 View Solution
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
AMRω4tBMRω2tCMRωtDMRωt - Question 2 - Select One
A disc has mass 'M" and radius 'R'. How much tangential force should be applied to the rim of the disc so as to rotate with angular velocity ω in time 't'?
AMrω4tBMRω2tCMRωtDMRωt - Question 3 - Select One
A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
AMRω4tBMRω2tCMRωtDMRωt
A thin capillary of inner radius r1 and outer radius r2 (The inner tube is solid) is dipped in water. To how much height will the water raise in the tube ? (Assume contact angle θ→0)
View SolutionA spherical conducting shell of inner radius R1 and outer radius R2 has charge Q. Now a charge q is placed inside the shell but not at centre then surface charge densities with their nature on inner and outer surfaces of shell are respectively.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q:
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero even if the shell is not spherical, but has any irregular shape? Explain.View SolutionA charge +q is placed somewhere inside the cavity of a thick conducting spherical shell of inner radius R1 and outer radius R2. A charge – Q is placed at a distance r>R2 from the centre of the shell. Then the electric field in the hollow cavity-
View Solution

