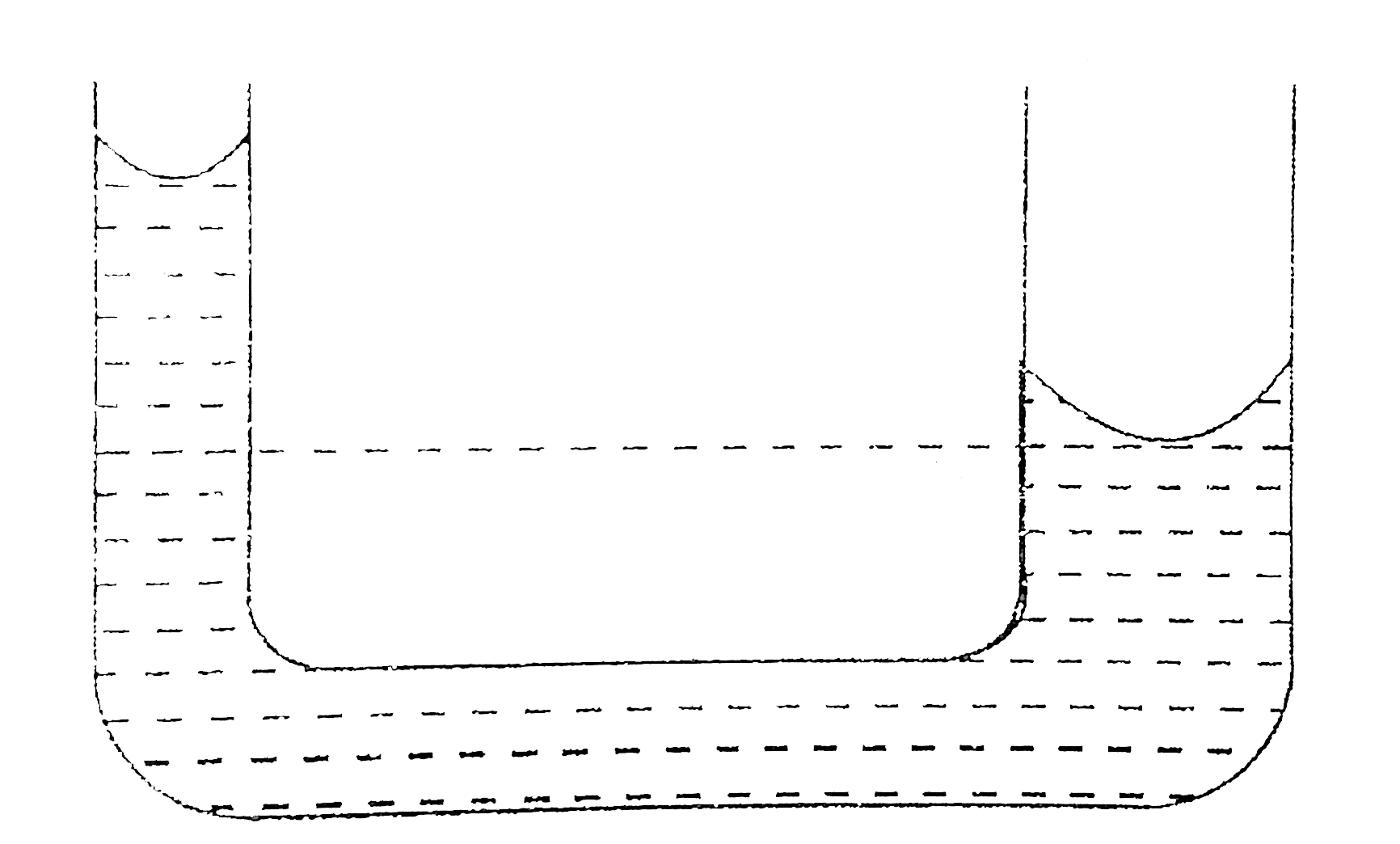
In the U−tube, radius of one arm is R and the other arm is 2R. Find the difference in water level if contact angle is θ=60∘ and surface tension of water is T.
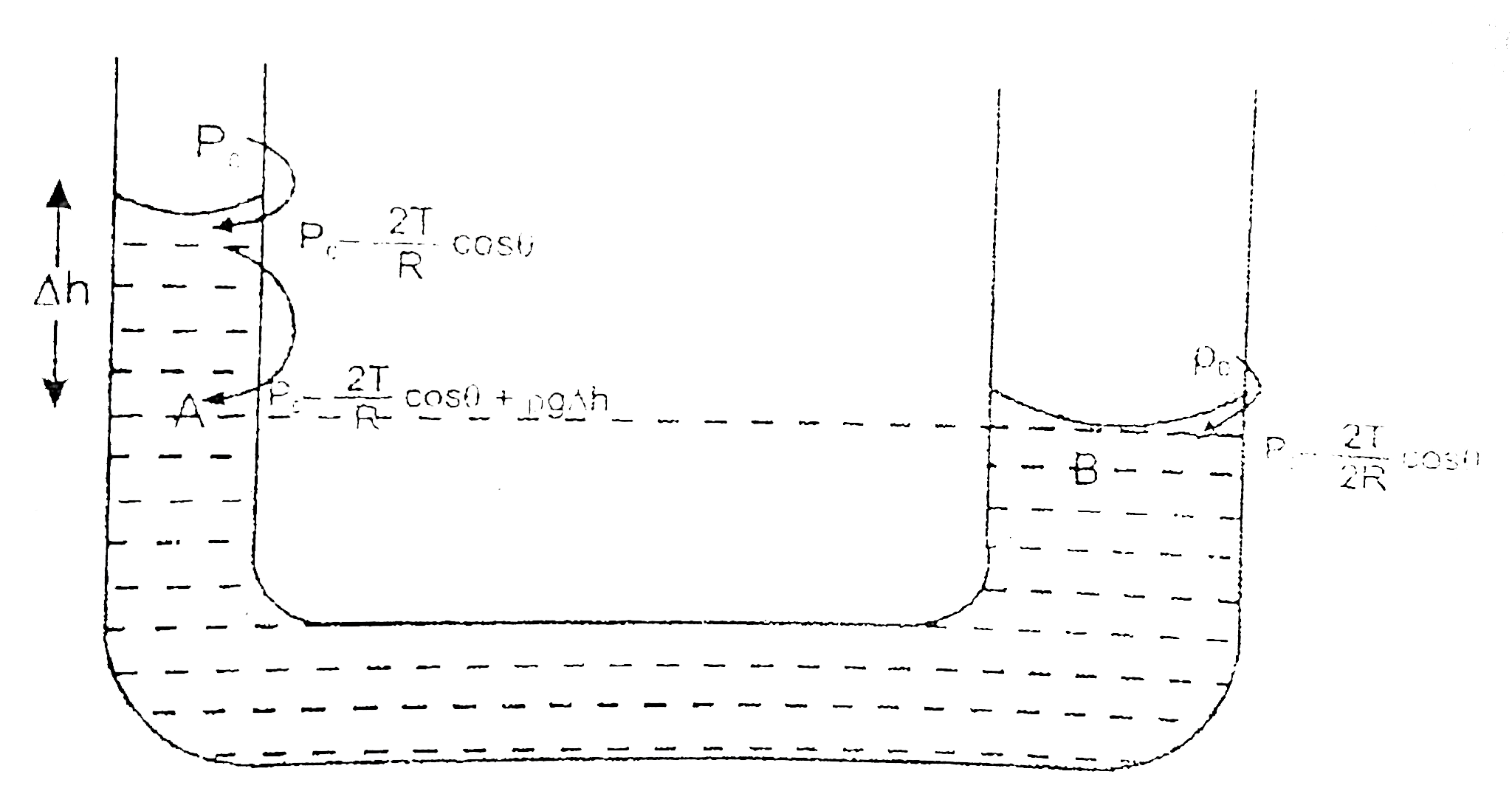
Balancing pressure at points A and B situated in same horizontal level.
P0−2TRcosθ+ρgΔh=P0−2T2Rcosθ
here θ=60∘, solving we get
Δh=T2ρgR
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I10videos
SURFACE TENSION
- BOOK - RESONANCECHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II17videos
SURFACE TENSION
- BOOK - RESONANCECHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
- BOOK - RESONANCECHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise27videos
UNITS, DIMENSION & MEASUREMENT
Similar Questions
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water =0.075Jm−2.
View SolutionTwo capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
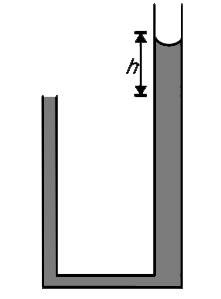
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .View Solution
Knowledge Check
- Question 1 - Select One
Two capillary tubes of diameters 3.0mm and 6.0mm are joined together to form a U-tube open at both ends. If the U-tube is filled with water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3×102N/m. Take the angie of contact to be zero and density of water to be 103kg/m3(g=9.8m/s2)
A5mmB10mmC15mmD20mm - Question 2 - Select One
A drop of radius r is broken into n equal drips. Calulate the work done if surface tension of water is T.
A4rπR2nTB4rπR2T(n2/3−1)C4rπR2T(n1/3−1)DNone of the above - Question 3 - Select One
A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle θ with vertical edge of the disc. If the disc displaces a weight of water W and surface tension of water is T, then the weight of metal disc is :
A2πrT+WB2πrTcosθ−WC2πrTcosθ+WDW−2πrTcosθ
Two narrow bores of diameters 3.0mm and 6.0 mm are joined together to form a U-shaped tube open at both ends. If th U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3×10−2Nm−1. Take the angle of contact to be zero. and density of water to be 1.0×103kg/m3.
(g=9.8ms−2)View SolutionA glass U−tube is inverted with open ends of the straight limbs, of diameters 0.5mm and 1.0mm below the surface of water in a beaker. The air pressure in the upper part is increased until the meniscus in one limb is level with the water outside. Find the height (cm) of water in the other limb in nearest integer. : (Density of water is 103Kg/m3 and surface tension of water is 7.5×10−2N/m. Take contact angle θ=0∘)
 View Solution
View SolutionA small air bubble of radius r in water is at depth h below the water surface. If P0 is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
View SolutionWhat is the weight of water raised inside the capillary tube of radius 0.4mm?(Take angle of contact of water with glass as 0∘, surface tension of water 70dynecm−1)
View SolutionA narrow tube of length l and radius r is sealed at one end. Its open end is brought in contact with the surface of water while the tube is held vertical. The water rises to a height h in the tube. The contact angle of water with the tube wall is θ, density of water is ρ and the atmospheric pressure is Po. Find the surface tension of the liquid. Assume that the temperature of air inside the tube remains constant and the volume of the meniscus is negligible.
View Solution

