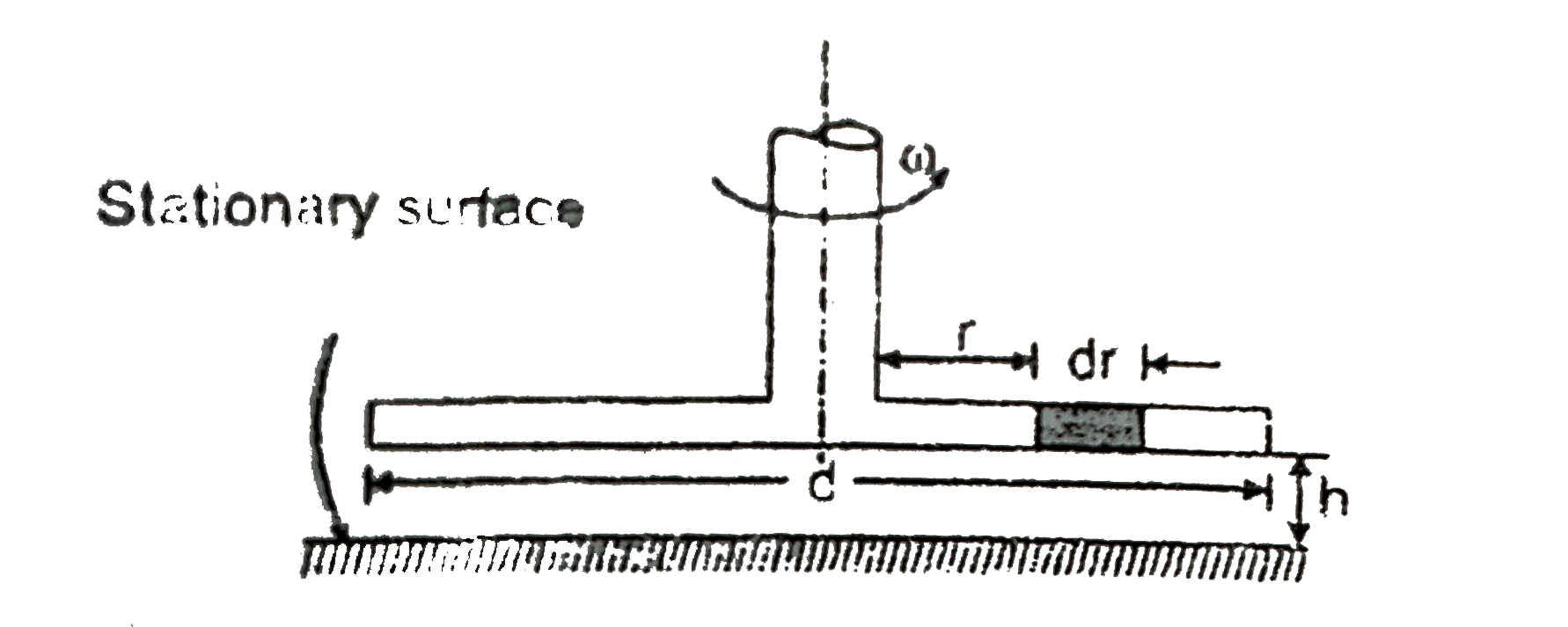
A circular disc of a diameter 'd' slowly rotated in a liquid of large 'η' at a small distance 'h' from a fixed surface as shown in figure. If an expression for torque 'τ' necessary to maintain an angular velocity 'ω' is πηd4λh then fidn λ.
The correct Answer is:32
dt=η(2πrdrωrh)
t=r∫0ηh2πωr3dr⇒t=∫d/20ηωh2πr3dr
t=[2πηωhr44]d/20⇒t=2πηωhd44×16
t=(πηωd432h)
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - III
11 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - I
7 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - I
11 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
43 Videos
Similar Questions
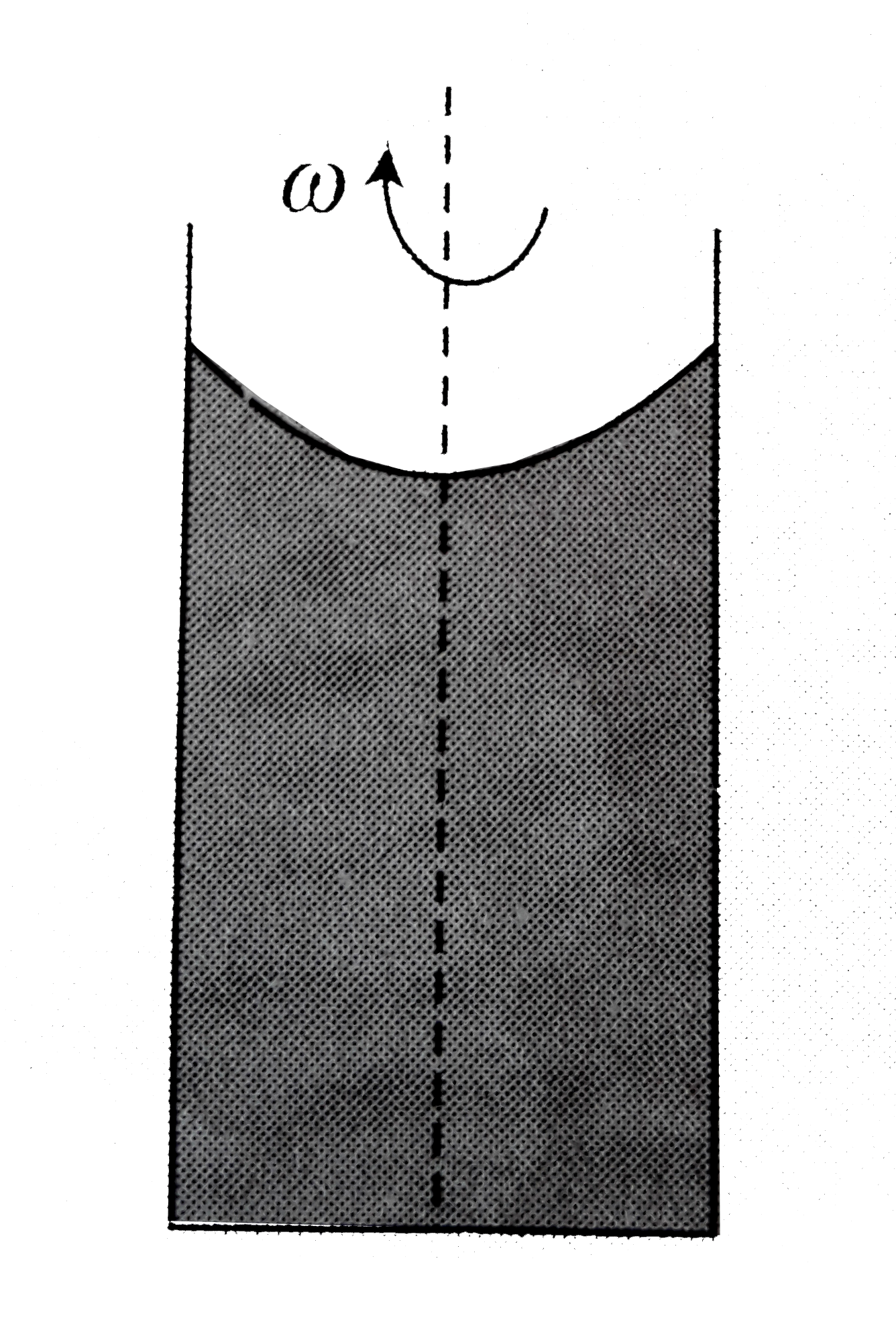
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
 .
.
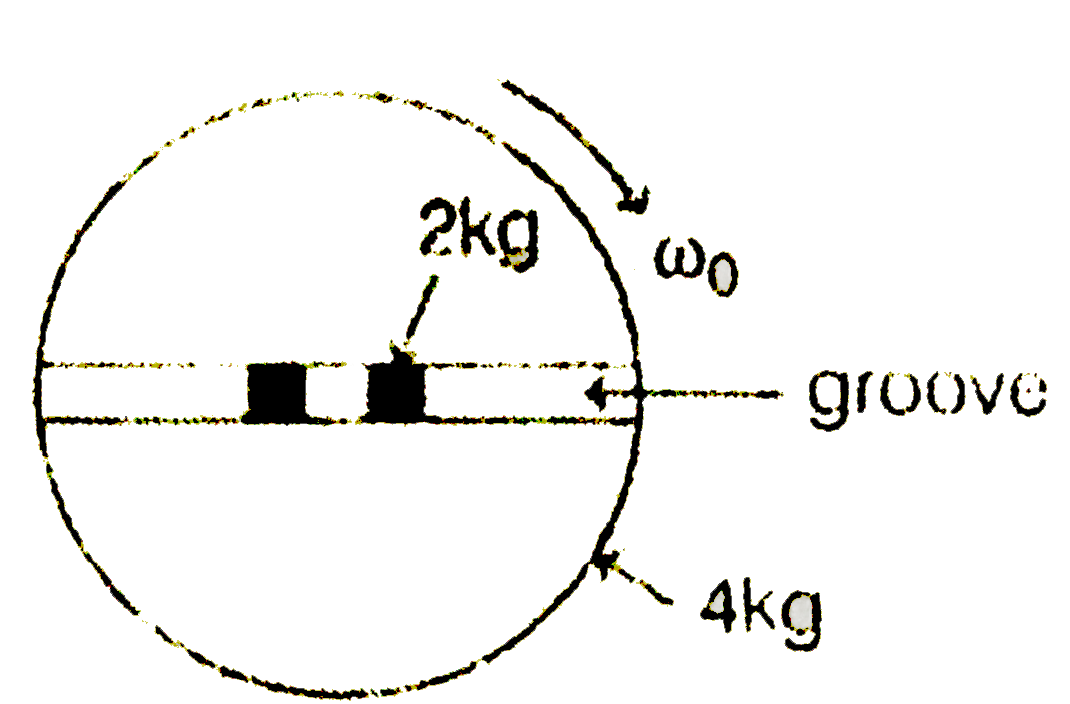
View SolutionA disc of mass 4kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass 2kgeachareplaced∈itoneithersofthecentreofthediscasshown∈figure.Thediscisgiven∈itialanga––rvelocityomega_(0)=12 (rad) / (s) released. Find the angular speed of disc (in radian/s) when the balls reach the ends to disc.
'(##CEN_KSR_PHY_JEE_C09_E01_016_Q06##)'
View Solution
Knowledge Check
A large rectangular box has been rotated with a constant angular velocity ω1 about its axis as shown in the figure. Another small box kept inside the bigger box is rotated in the same sense with angular velocity ω2 about its axis (which is fixed to floor of bigger box). A particle P has been identified, its angular velocity about AB would be
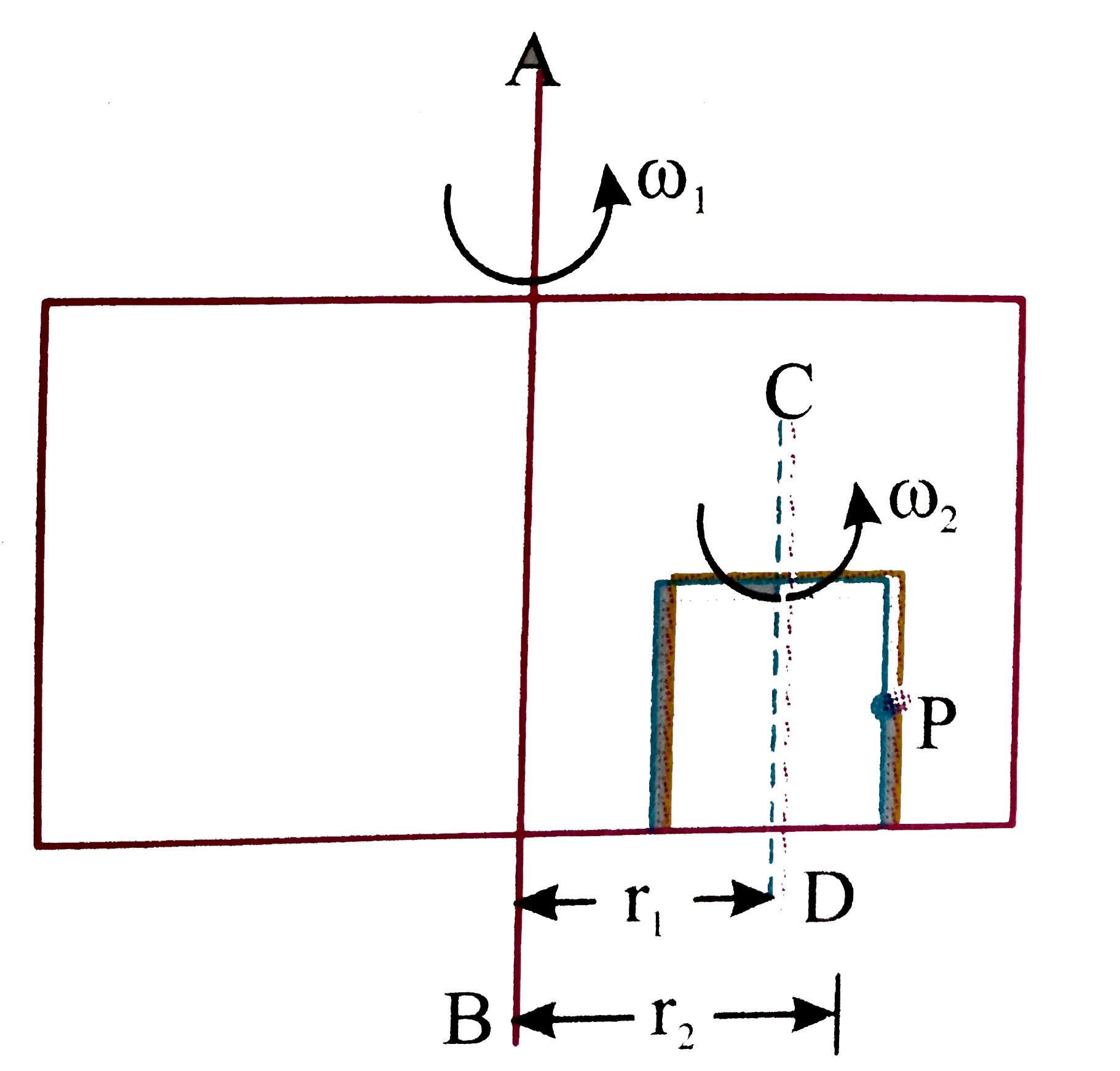 Aω2(r2−r1)+ω1r2r2Bω2(r2−r1)+ω1r1r2Cω1Dω2
Aω2(r2−r1)+ω1r2r2Bω2(r2−r1)+ω1r1r2Cω1Dω2A disc of mass 'm' and radius R is free to rotate in horizontal plane about a vetical smooth fixed axis passing through is centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in fig. The disc is given initial angular velocity ω0 and released. The angular speed of the disc when the balls reach the end of the disc is -
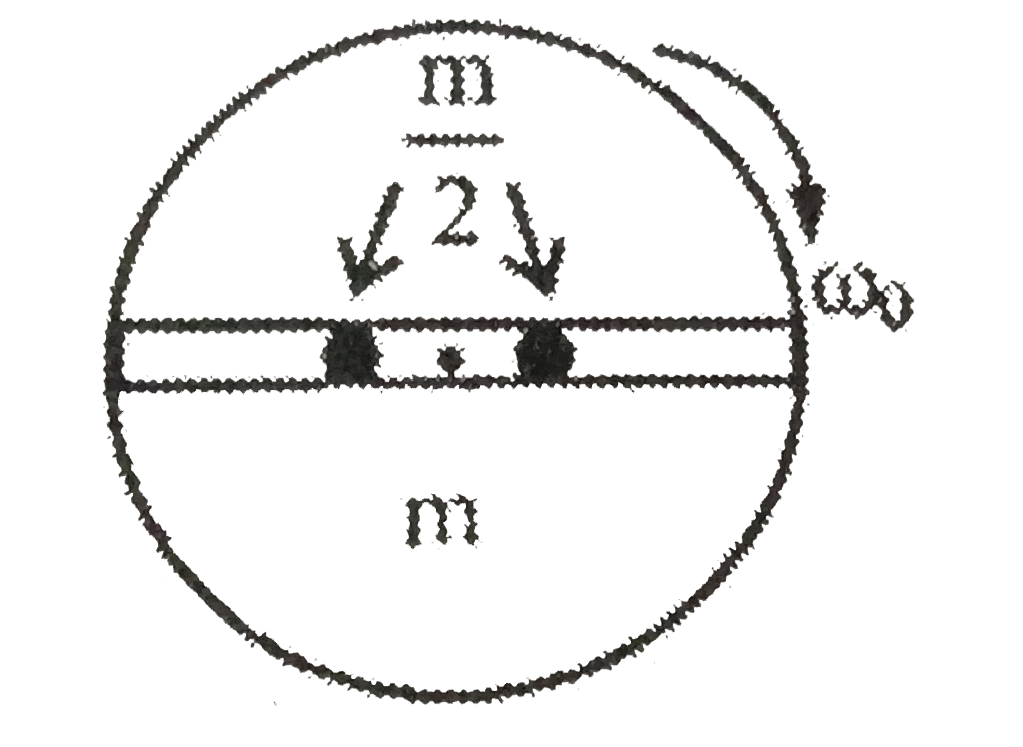 Aω02Bω03C2ω03Dω04
Aω02Bω03C2ω03Dω04A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc isAω02Bω03C2ω03Dω04
A uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionSelect ALL correct answer :
A disc of radius R is placed over a horizontal table in such a way that plane of the disc is horizontal and rotated about its vertical axis passing through its center with angular velocity ω. A layer of grease of thickness l is present between the table and the disc.Coefficient of viscosity of grease is η .Then,
(A) torque needed to rotate the disc with constant angular velocity is πηωR44l
(B) torque needed to rotate the disc with constant angular velocity is πηωR42l
(C) power needed to rotate the disc with constant angular velocity is πηω2R42l
(D) power needed to rotate the disc with constant angular velocity is πnω2R44l
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
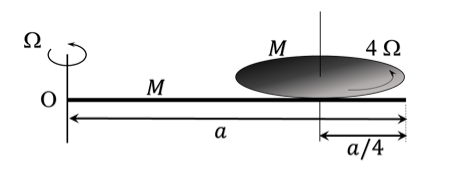
View SolutionA thin rod of mass M and length a is free to rotate in horizontal plane about a fixed vertical axis passing through point O. A thin circular disc of mass M and of radius a/4 is pivoted on this rod with its center at a distance a/4 from the free end so that it can rotate freely about its vertical axis. Assume that both rod and disc have uniform density and they remain horizontal during motion. An outside stationary observer finds the rod rotating with an angular velocity Ω and the disc rotating about its vertical axis with angular velocity 4Ω. Total angular momentum of system about point O is (Ma2Ω48)n. The value of n is
View SolutionA small block of mass m is tied to the top of a smooth inclined plane with the help of a string of length L as shown in the figure. The inclined plane of inclination θ with horizontal is rotated with an angular velocity ω about a verticle axis passing through the end of the string fixed to the plane.
(a) Find the maximum value of ω so that the block maintains contact with the inclined plane.
(b) Find the ratio of the tension in the string and the normal reaction between the block and the plane.

View Solution
