If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
1:2:3
1:3:5
1:1/2:1/3
1:1/3:1/5
The correct Answer is:C
To find the ratio of the wavelengths λ1:λ2:λ3 for the fundamental frequency and the first and second overtone modes in an open organ pipe, we can follow these steps:
Step 1: Understand the relationship between frequency and wavelength
In an open organ pipe, the fundamental frequency (first harmonic) corresponds to one wavelength fitting in the length of the pipe, while the first overtone (second harmonic) corresponds to two wavelengths fitting in the length of the pipe, and the second overtone (third harmonic) corresponds to three wavelengths fitting in the length of the pipe.
Step 2: Write the equations for the wavelengths
For an open organ pipe:
- Fundamental frequency (first harmonic):
L=λ12⟹λ1=2L
- First overtone (second harmonic):
L=2λ22⟹λ2=L
- Second overtone (third harmonic):
L=3λ32⟹λ3=2L3
Step 3: Write the ratio of the wavelengths
Now we can express the wavelengths in terms of L:
- λ1=2L
- λ2=L
- λ3=2L3
Now, we can write the ratio:
λ1:λ2:λ3=2L:L:2L3
Step 4: Simplify the ratio
To simplify the ratio, we can eliminate L from all terms:
=2:1:23
To express all terms with a common denominator, we can multiply through by 3:
=2×3:1×3:23×3=6:3:2
Step 5: Final ratio
Thus, the final ratio of the wavelengths is:
λ1:λ2:λ3=6:3:2
In an open organ pipe, the fundamental frequency (first harmonic) corresponds to one wavelength fitting in the length of the pipe, while the first overtone (second harmonic) corresponds to two wavelengths fitting in the length of the pipe, and the second overtone (third harmonic) corresponds to three wavelengths fitting in the length of the pipe.
For an open organ pipe:
- Fundamental frequency (first harmonic):
L=λ12⟹λ1=2L
- First overtone (second harmonic):
L=2λ22⟹λ2=L
- Second overtone (third harmonic):
L=3λ32⟹λ3=2L3
Now we can express the wavelengths in terms of L:
- λ1=2L
- λ2=L
- λ3=2L3
λ1:λ2:λ3=2L:L:2L3
To simplify the ratio, we can eliminate L from all terms:
=2:1:23
=2×3:1×3:23×3=6:3:2
Thus, the final ratio of the wavelengths is:
λ1:λ2:λ3=6:3:2
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I25videos
SOUND WAVES
- BOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - II20videos
SOUND WAVES
- BOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - I34videos
SOUND WAVES
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise28videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
A1:2:3B1:3:5C1:1/2:1/3D1:1/3:1/5 - Question 2 - Select One
If λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
A1:2:3B1:13:15C1:3:5D5:3:1 - Question 3 - Select One
If λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
A1:2:3B1:3:5C1:12:13D1:13:15
Some energy levels of a molecule are shown in the fig. The ratio of the wavelengths r=λ1/λ2, is given by
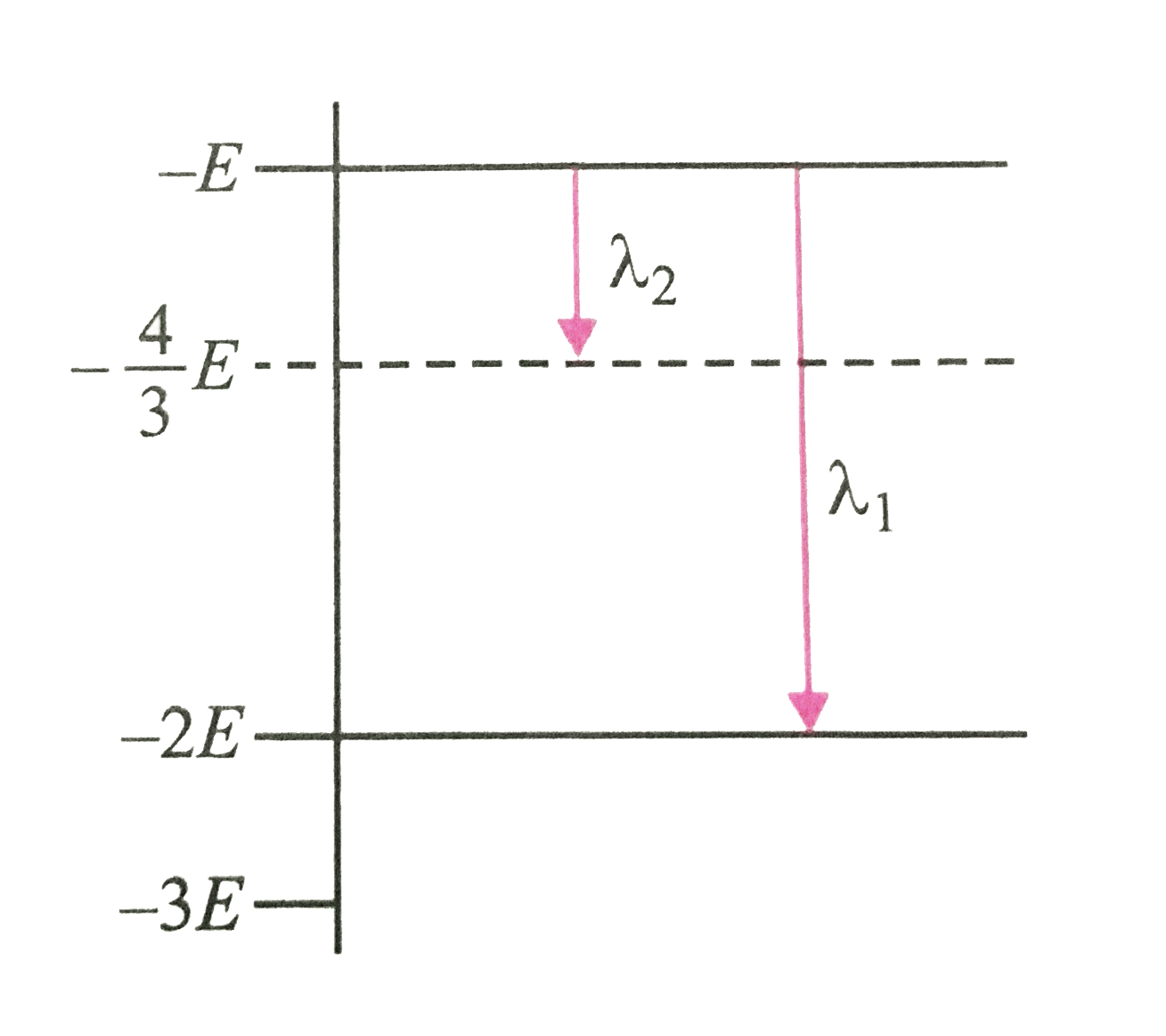 View Solution
View SolutionThree energy levels P,Q,R of a certain atom are such that EP<EQ<ER. Ifλ1,λ2andλ3 are the wave length of radiation to transition R→Q,Q→P and R→P respectively . The correct relationship between λ1,λ2and,λ3 is
View SolutionThe wavelength of electron waves in two orbits (λ1:λ2)
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View SolutionIf λ1andλ2 are the wavelength of the first members of the Lyman and Paschen series, respectively , then λ1λ2 is
View Solution

