The As-CI bond distance in AsCI3 is 2.20Å. Estimate the SBCR (single bond covalent radius) of As. (Assume EN of both to be same and radius of CI=0.99Å).
The correct Answer is:[1.21Å]
[dAs−Cl=rAs+rCl
2.20=rAs+0.99
rAs=1.21Å]
Topper's Solved these Questions
Similar Questions
Arrange C−C,C=C and C≡C in order of
(i) Decreasing bond energey
(ii) Decreasing bond lengths
(b) The As−CI bond distance in AsCI3 is 2.20A Estimate the single- bond covalent radius of As .View SolutionThe bond distance between C-Cl in CCl4 is 1.76 Å. If atomic radius of C is 0.77Å. Determine the atomic radius of Cl to the nearest integer (round off). (Given E.N. Of C is 2.5 and Cl is 3.0)
View Solution
Knowledge Check
- Question 1 - Select One
if the radius of H is 0.53Å then what will be the radius of .3Li2+ ?
A0.17ÅB0.36ÅC0.53ÅD0.59Å - Question 2 - Select One
Covalent radius of Ci si 99 pm. Select best representation for CI2 molecule:
A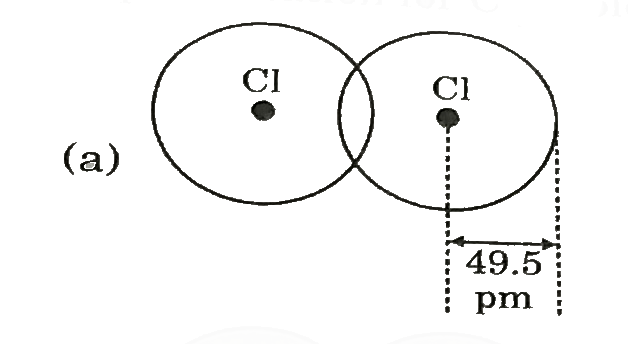 B
B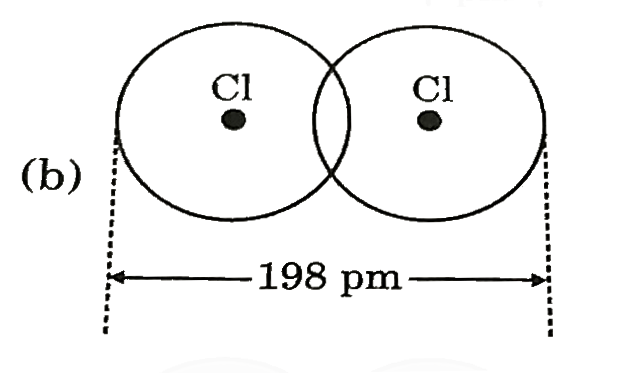 C
C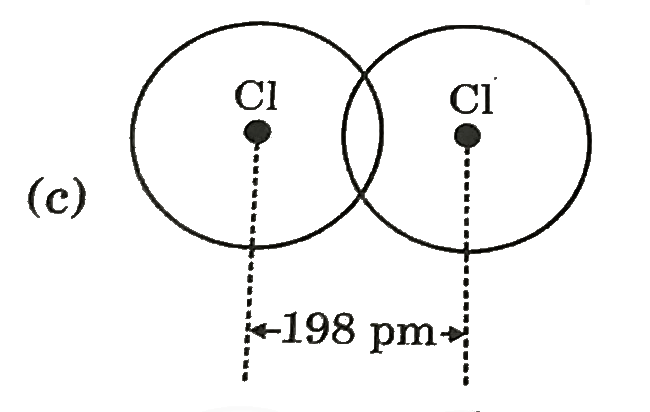 D
D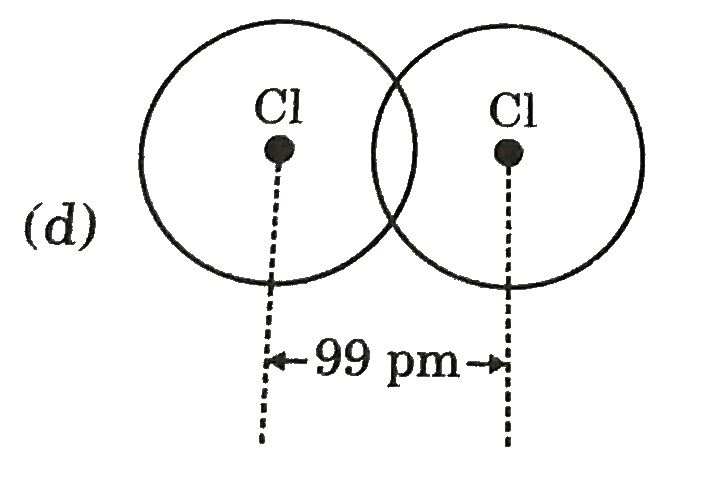
- Question 3 - Select One
If the bond distance in chlorine molecule (Cl_2) is 198 pmthen the radius of chlorine is
A198pmB49.5pmC99pmD24.75pm
Calculate the percentage of covalent character of HX having bond length = 1.62 Å and observed dipole moment = 0.39 D.
View SolutionThe ionic radii of F− and O2− respectively are 1.33 Å and 1.4 Å, while the covalent radius of N is 0.74 Å.
The correct statement for the ionic radius of N3− from the following is :View SolutionFor chlorine molecule, the CI−CI bond length is 198 pm. Find the convalent radius of chlorine?
Strategy: Use Eq. to obtain directly the convalent radius of chlorine atom.View SolutionThe covalent radius of hydrogen is 0.37A0. The bond length in H2 molecule is
View SolutionThe platinum-chlorine distance has been found to be 2.32Å in several crystalline compounds This value applies to both compounds A and B given here
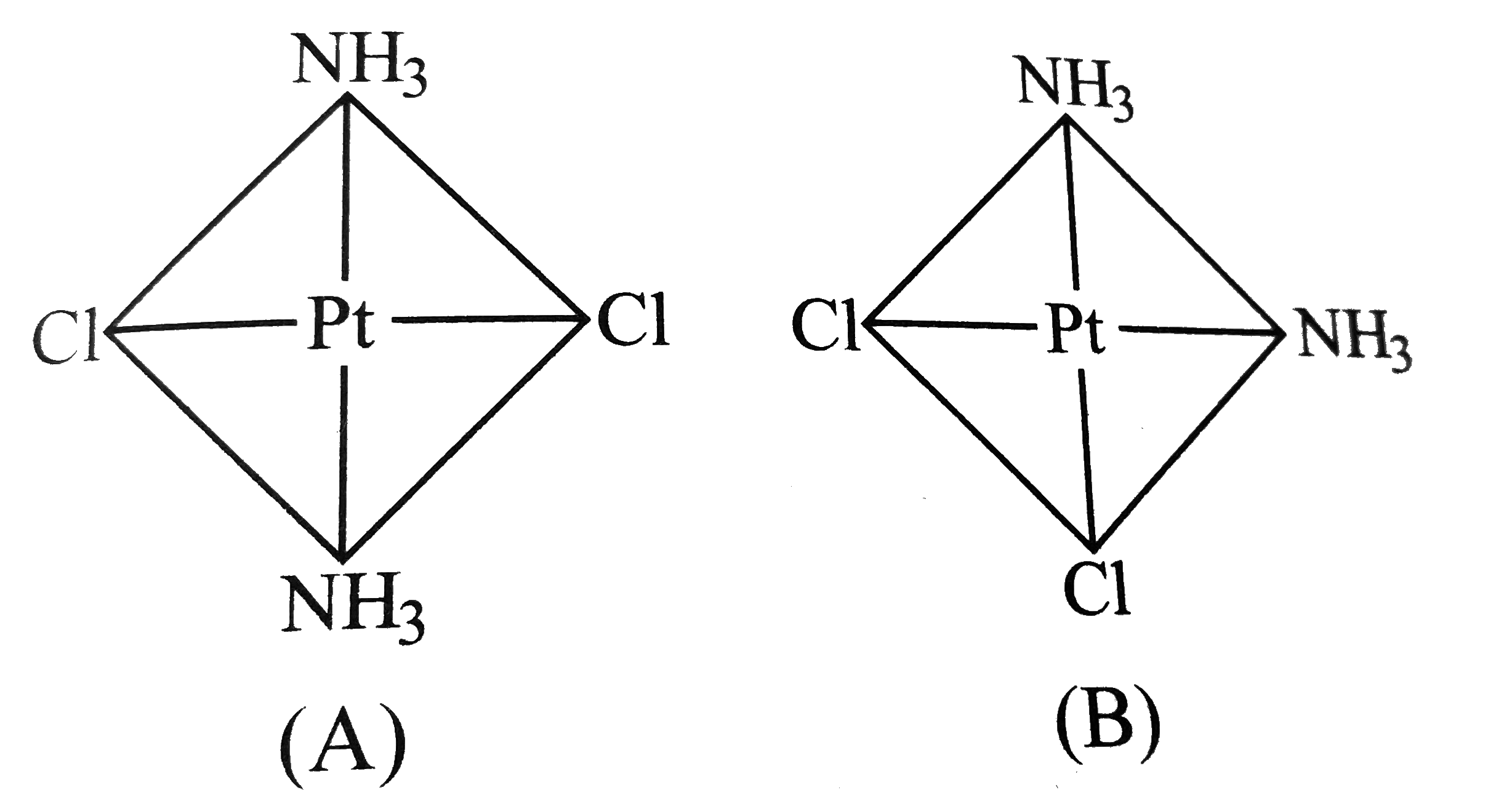

Based on the above structures, answer the following questions
The C−C single-bond distnaance is 1.54Å What is the distance between the terminal carbons is propane ? Assume that the four bonds of any carbon atoms arre pointed towards the corners of a reqular tetrahedron .View Solution

