A small mass m is transferred from the centre of a hollow sphere of mass M to infinity. Find work done in the process. Compare this with the situation if instead of a hollow sphere, a solid sphere of same mass were there.
We know at infinity gravitional potential is taken zero. Thus if VC be the gravitational potential at centre of holow sphere then external work required the procedd is
W=m(0−VC)
or =m(0−(GMR))=GMmR
Here VC=−GMR, the potential at the centre of a hollow sphere of mass M and radius R. If a so solid sphere is here, we have at its centre
VC=−32GMR
Thus work required will be
W=m[0−(−32GMR)]=32GMmR
We can see in second case more work is required for the process.
Topper's Solved these Questions
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Solved Example
8 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Practice Exercise
18 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- HEAT TRANSFERBOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise
89 Videos
Similar Questions
Knowledge Check
The ratio of the radii of gyration of a hollow sphere and a solid sphere of the same radii about a
A√73B5√21C√215D259A mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
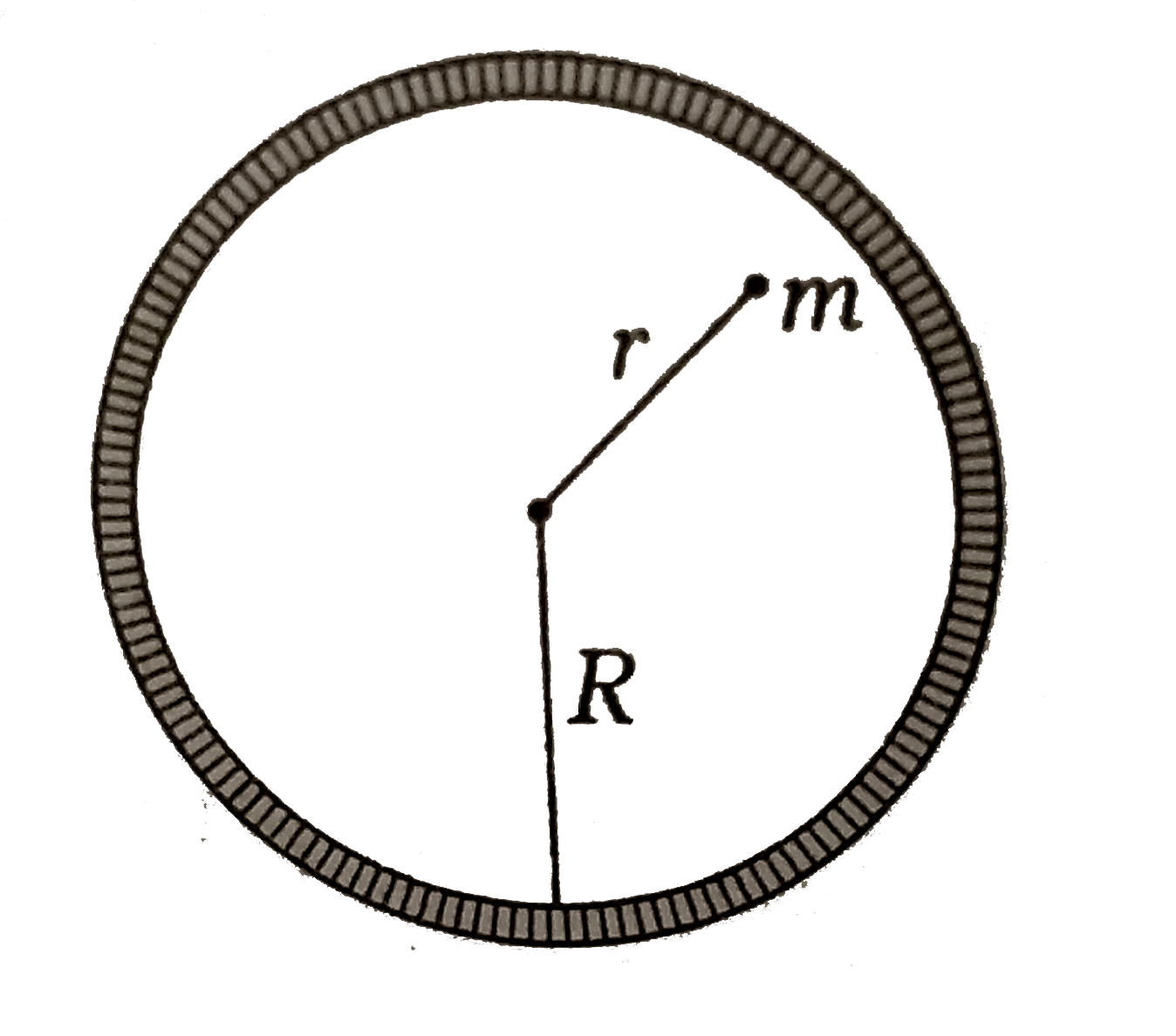 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2DzeroA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
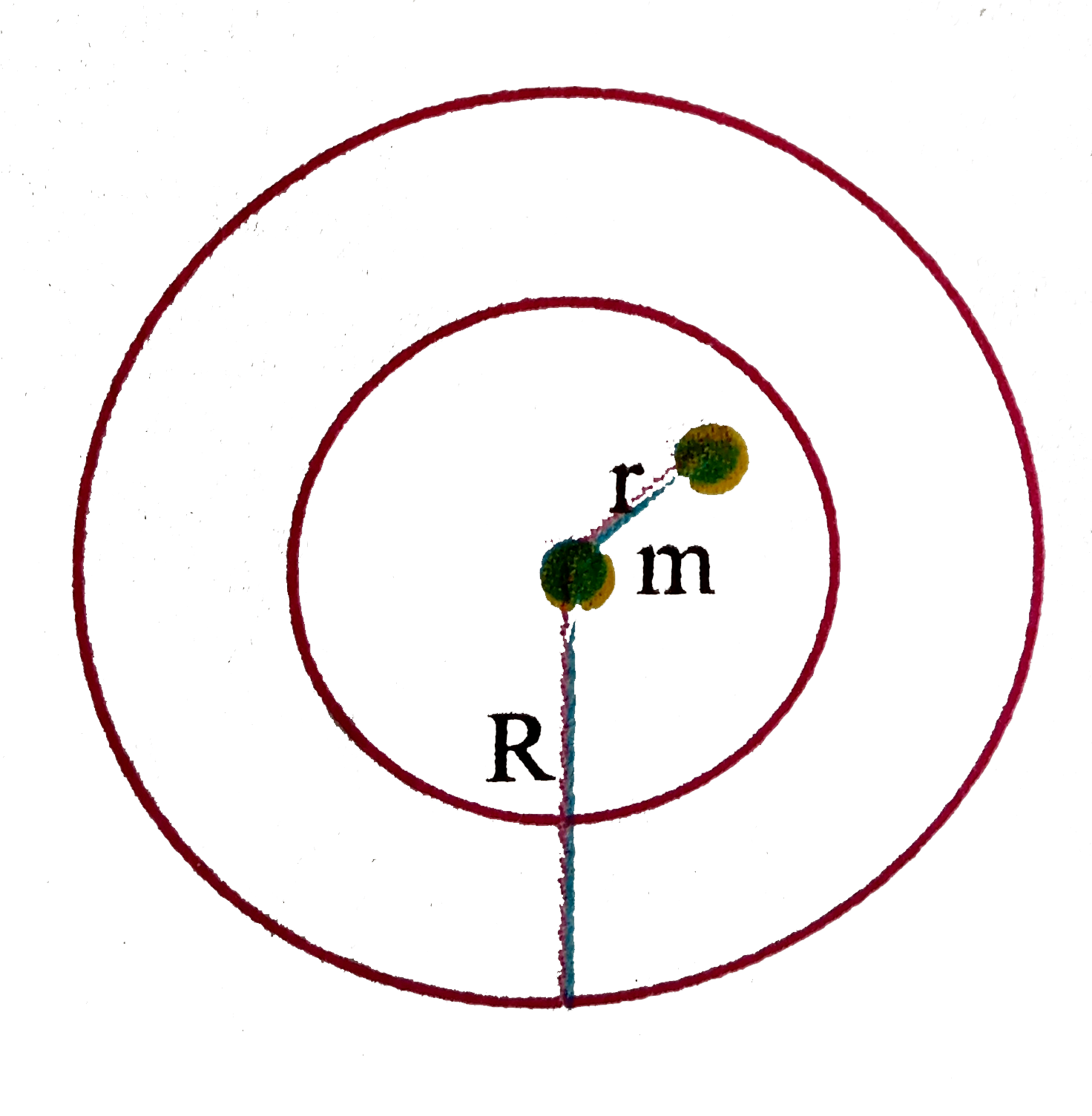 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero
A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
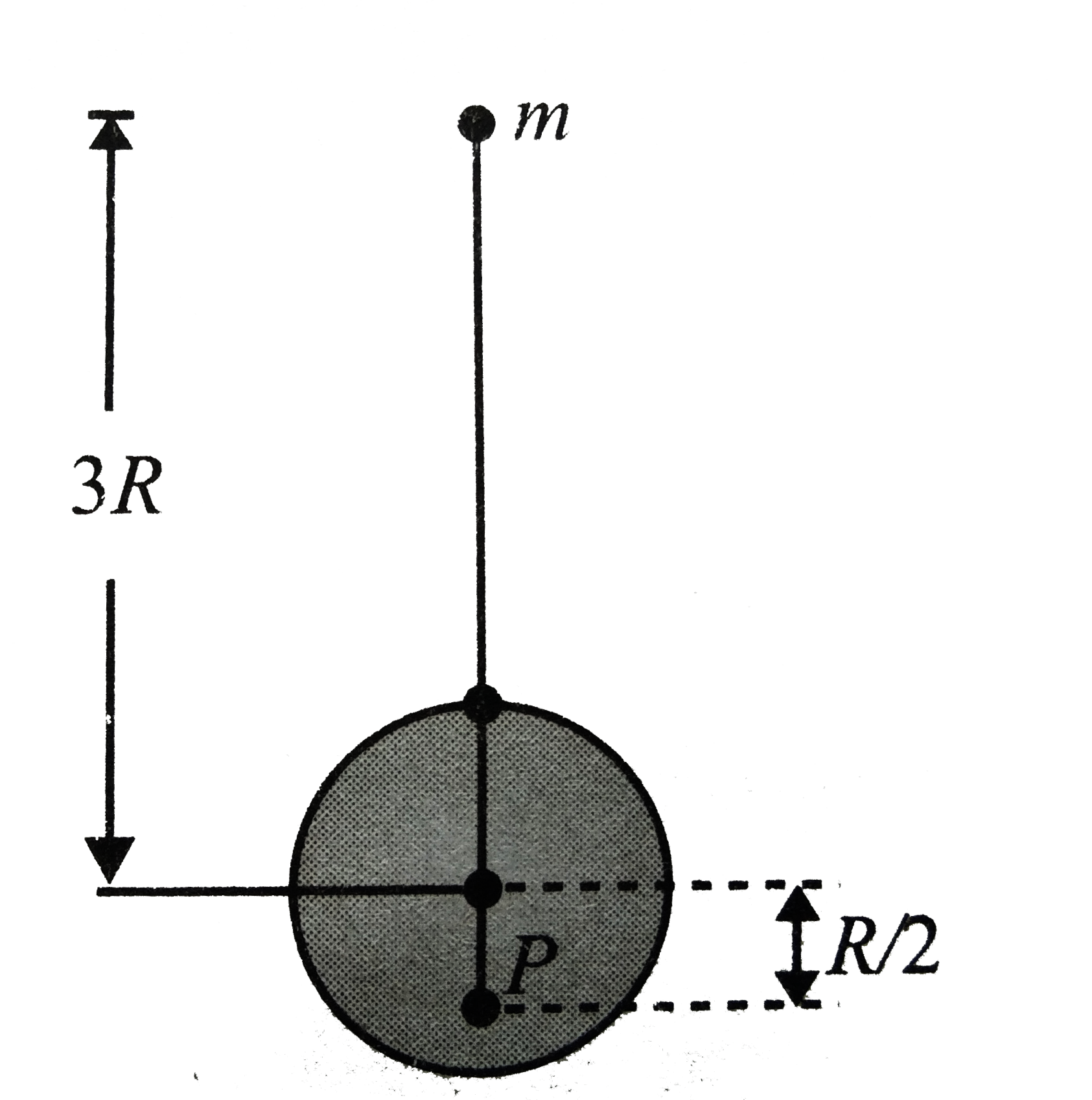
View SolutionA hollow spherre is released from rest on a rough inclined plane as shown in the figure. Find the velocity of point of contact as a function of time. ( m = mass of hollow sphere, R = radius of sphere )

View SolutionA point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is

View SolutionA hollow spherre is released from rest on a rough inclined plane as shown in the figure. Find the velocity of point of contact as a function of time. ( m = mass of hollow sphere, R = radius of sphere )

View SolutionA spherical hollow cavity is made in a lead sphere of radius R such that is surface touches the outside surface of the lead sphere and passes through its centre. The mass of the sphere before hollowing was M with what gravitational force will the hollowed out lead sphere attract a small sphere of mass m which lies at a distacne d from the centre of the lead sphere on the straight line connecting the centeres of the spheres and that of the hollow if d=2R
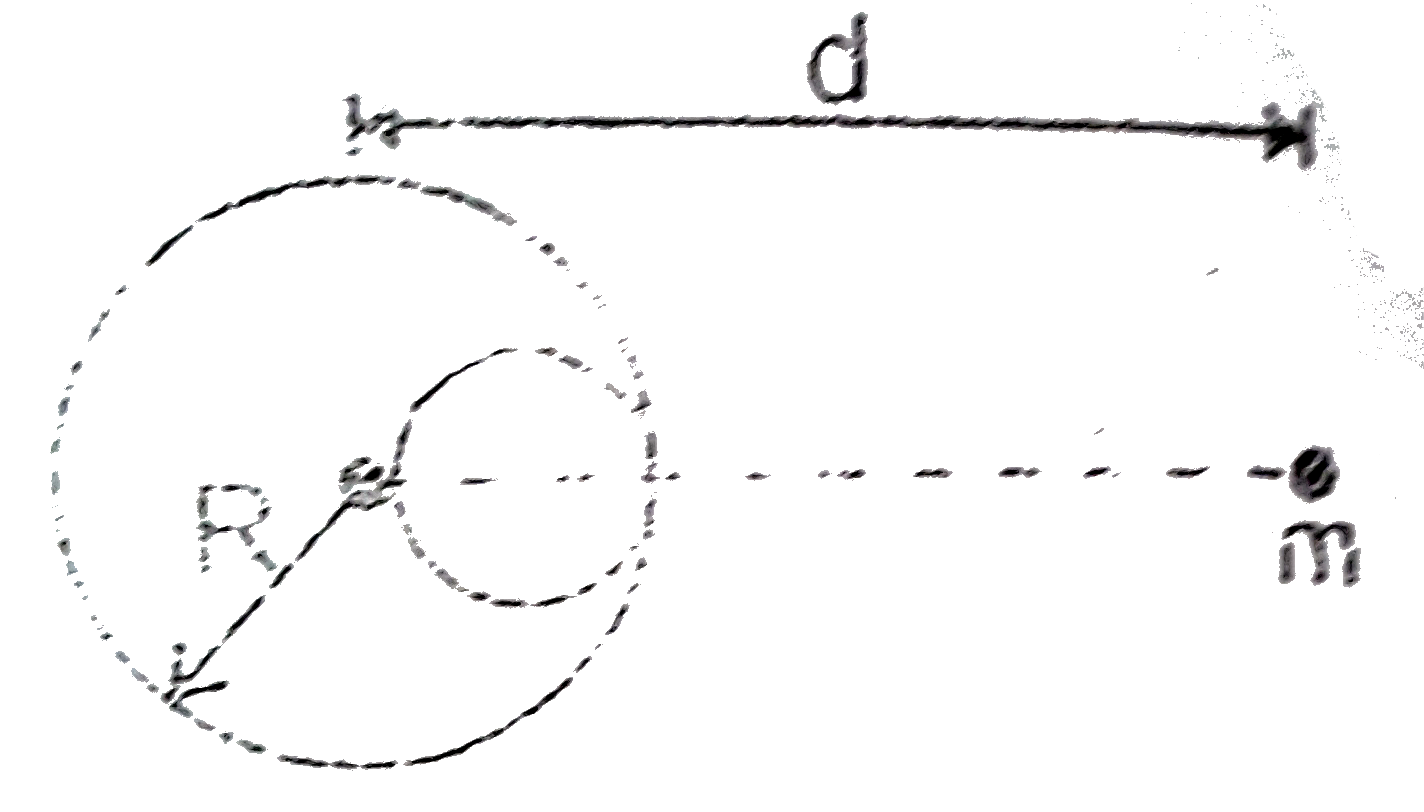 .
.
View Solution
