A planet revolves about the sun in elliptical orbit. The arial velocity (dAdt) of the planet is 4.0×1016m2/s. The least distance between planet and the sun is 2×1012m. Then the maximum speed of the planet in km/s is -
10
20
40
None of these
The correct Answer is:C
dAdt=r2ω2 is constant
∴dAdt=r2maxωmin2=r2minωmax2
⇒ωmin=2dA/dtr2max
Vmax=ωminrmin=2dA/dtrmin=40km/s
Topper's Solved these Questions
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -2 [Paragraph Type]
11 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -2 [Reasoning Type]
5 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Practice Exercise
18 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- HEAT TRANSFERBOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise
89 Videos
Similar Questions
A planet revolves about the sun in an elliptical orbit of semi-major axis 2×1012m. The areal velocity of the planet when it is nearest to the sun is 4.4×1016m/s. The least distance between the planet and the sun is 1.8×1012m/s. The minimum speed of the planet in km/s is 10K. determine the value of K.
View SolutionA planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
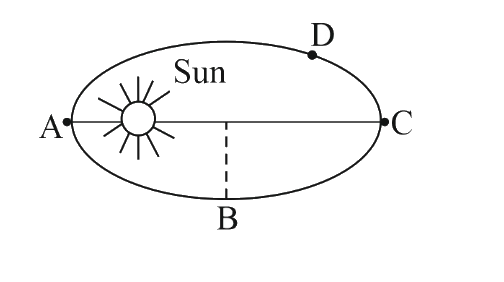
View Solution
Knowledge Check
A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
A|v×r|B2|r×v|C∣∣∣12(r×v)∣∣∣DNone of theseThe distance of two planets from the sun are 1013and1012 m respectively. The ratio of the periods of the planet is
A100B1√10C√10D10√10A planet is revolving round the sun in an elliptical orbit as shown in figure. Select correct alternative(s)
AIts total energy is negative at D.BIt s angular momentum is constantCNet torque on the planet about sun is zeroDLinear momentum of the planet is conserved
A planet revolves about the sun in an elliptical orbit of semi-major axis 2×1012m. The areal velocity of the planet when it is nearest to the sun is 4.4×1016m/s. The least distance between the planet and the sun is 1.8×1012m/s. The minimum speed of the planet in km/s is 10K. determine the value of K.
View SolutionA planet goes around the sun in an elliptical orbit. The minimum distance of the planet from the Sun is 2×1012m and the maximum speed of the planet in its path is 40kms−1. Find the rate at which its position vector relative to the sun sweeps area, when the planet is at a distance 2.2×1012 from the sun.
View SolutionFor a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
View SolutionThe distance of two planets from the sun are 1012mand1010m respectively. Then the ratio of their time periods is
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
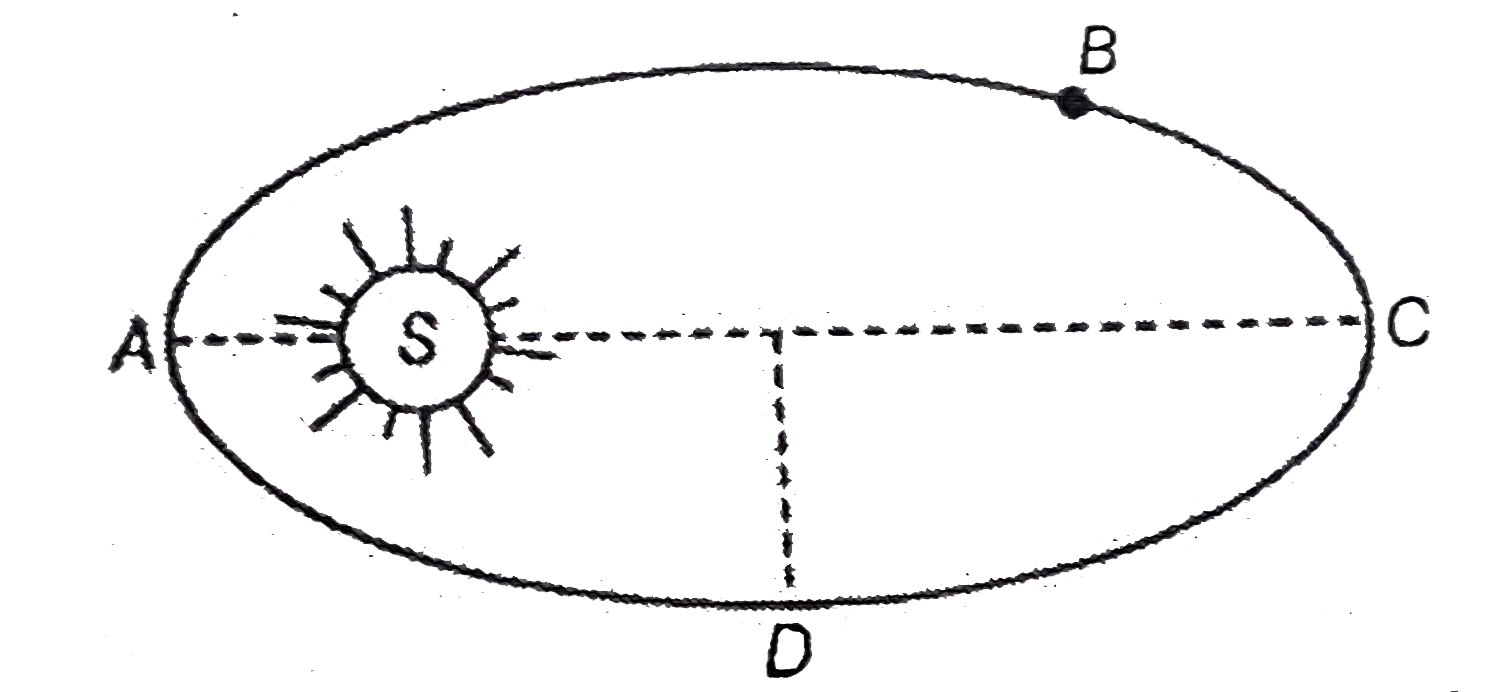
View Solution
