One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
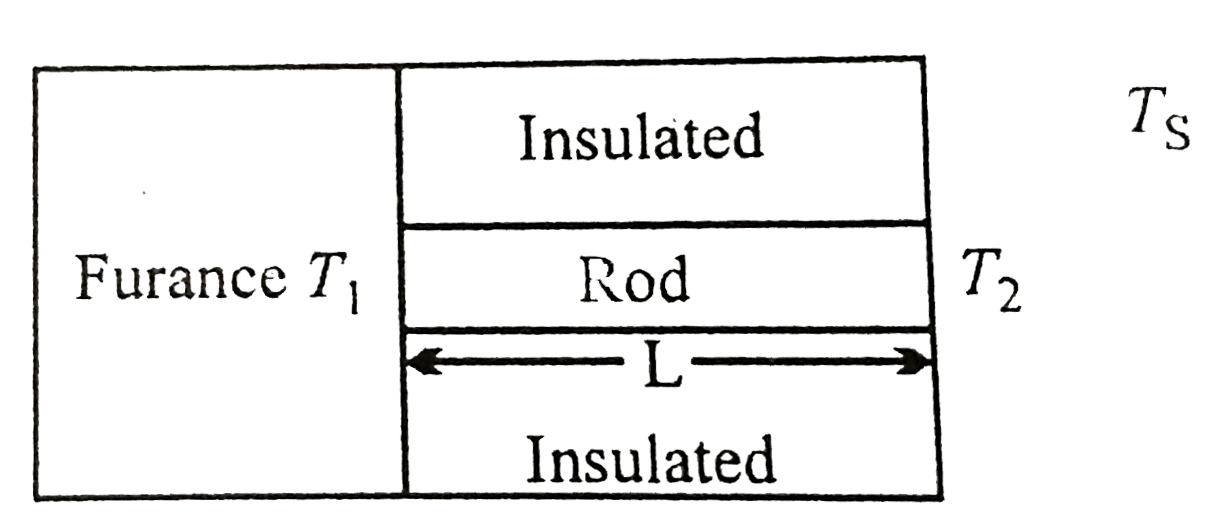
From the figure it is clear that emission takes place from the surface at temperture T2 (circular cross section). Heat conduction and radiation through laeral surface is zero.
Heat conducted through rod is
Q=KA(T1−T2)Δtl
Energy emitted by the surface of the rod in the same time Δt, is
E=εσA(T42−T4S)Δt
Since rod is at thermal equilibrium
∴E=Q
hence, KA(T1−T2)l=εσA(T42−T4S)Δt
⇒T1−T2=εσ(T42−T4S)K
Here T1−T2=ΔT and Ts>>ΔT
T1−(ΔT+TS)=εσlK[(ΔT+Ts)2−T4S]
T1−(ΔT+TS)=εσlK×T4S[(1+ΔTTS)4−1]
T1−(ΔT+TS)=εσlK×T4S[(1+4ΔTTS)4−1]
or T1−(TS+ΔT)=4εσlK×T3SΔT
or T−Ts=4εσlT3sKΔT+ΔT
or T1−Ts=(4εσlT3sK+1)ΔT
∴The∝ortionalityconstant= (1+4εσlT3sK)
Topper's Solved these Questions
Similar Questions
A cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T1 and the other end in surrounding at temperature T2. Surface of the rod exposed to the surrounding has emissivity e. Also T2=Ts+ΔTandTs>>ΔT. If T1−Ts∝ΔT,find the proportionality constant.
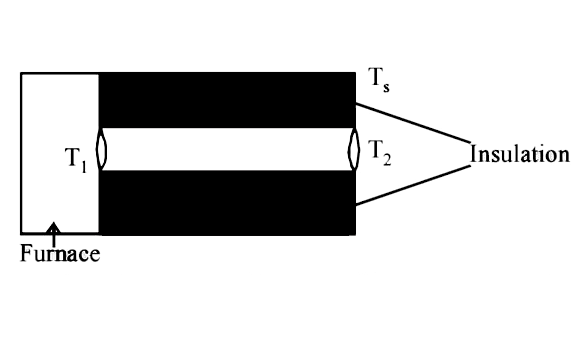
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View Solution
Knowledge Check
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
AdQdt=KL(T1−T2)ABdQdt=KL(T1−T2)LACdQdt=KLA(T1−T2)DdQdt=KA(T1−T2)LA solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
AT2−T1BT22−T21CT32−T31DT22−T41 .If TB and Ts are the temperatures of the body and the surroundings and TB−Ts is of very high value, then the rate of cooling in natural convection is proportional to .
AT4BBT4SC(TB−TS)54D(T54B−T54S)

Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
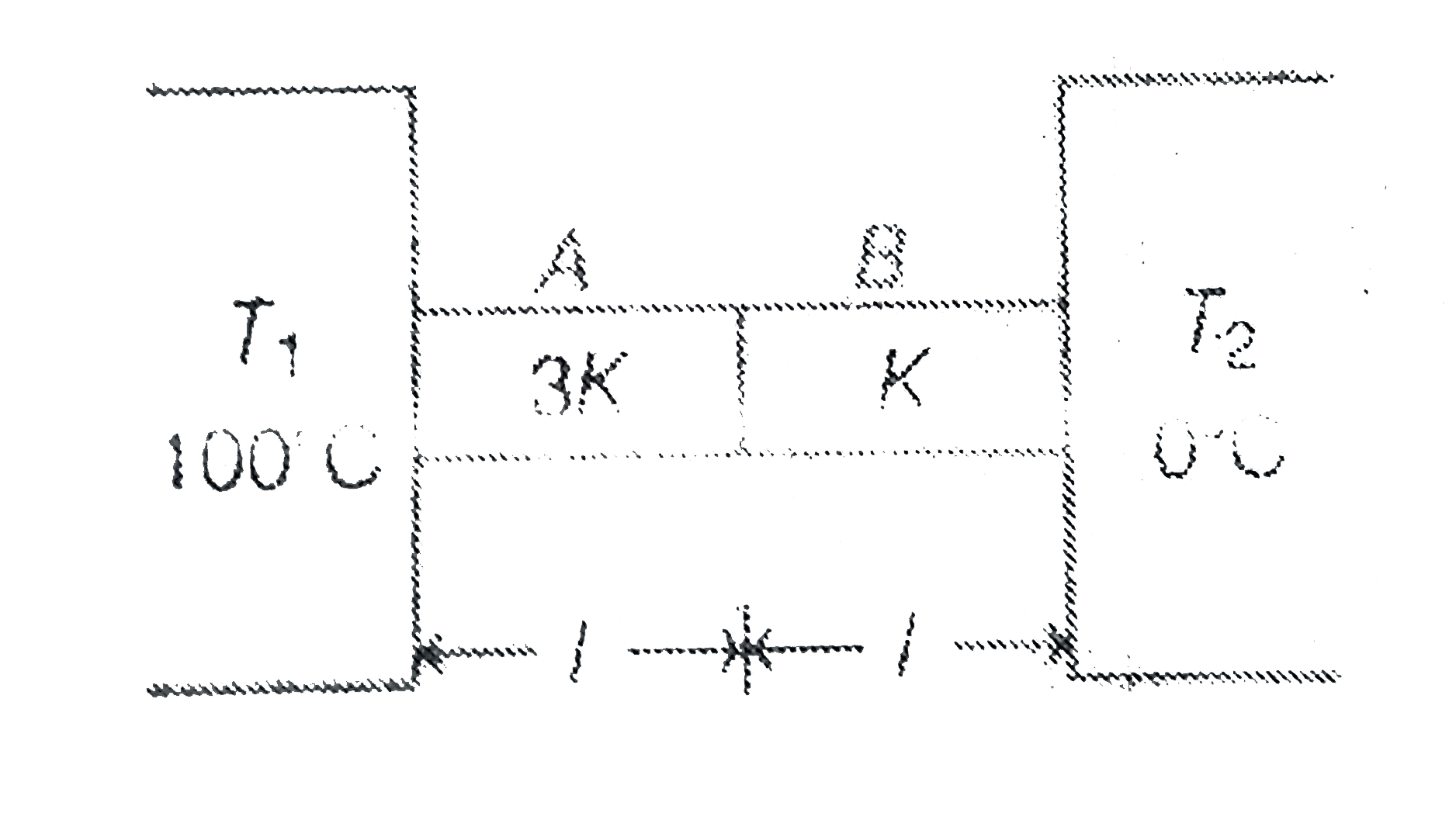
The ratio of the thermal resistance of the rods is
View Solution
