What is the angle between ?
(i) ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC
(ii) ¯¯¯¯¯¯ABand¯¯¯¯¯¯BC
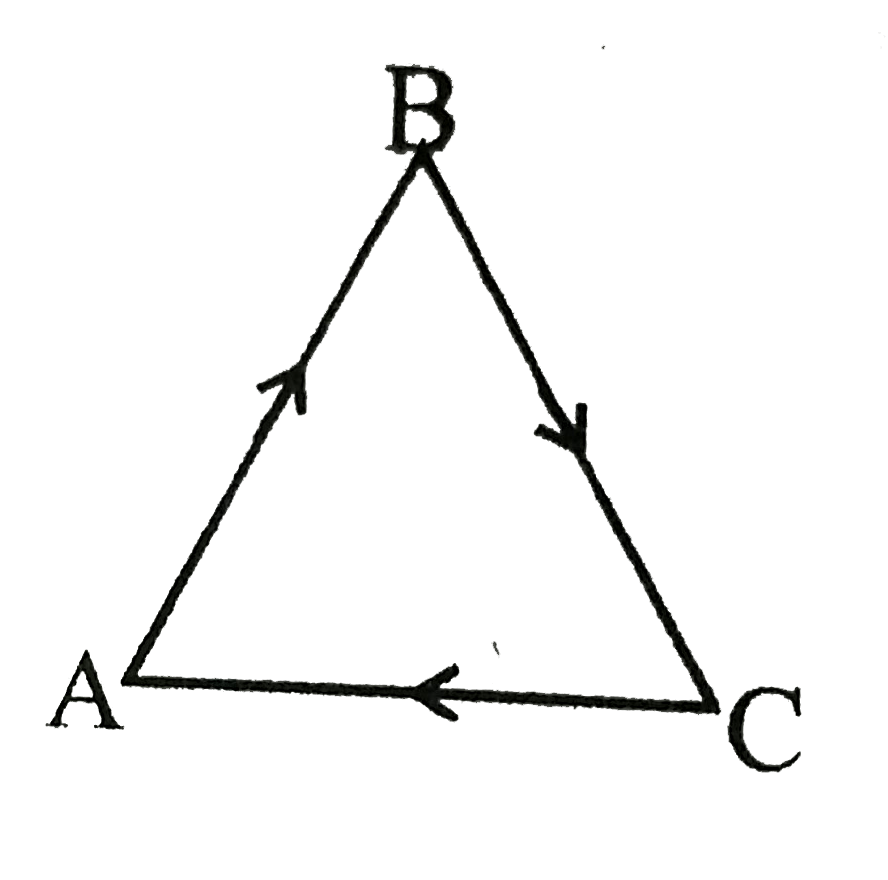
The correct Answer is:60∘ ,120∘
Step by step video, text & image solution for What is the angle between ? (i) bar(AB) and bar(AC) (ii) bar(AB ) and bar(BC) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:Solved Example
Explore 17 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:PRACTICE EXERCISE
Explore 4 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Section-B
Explore 13 Videos
Similar Questions
Knowledge Check
ΔABC is an isosceles triangle and ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=2aunit, ¯¯¯¯¯¯BC = a unit. Draw AD⊥BC, and find the length of ¯¯¯¯¯¯AD .
A√15 a unitB√152 a unitC√17 a unitD√172a unitIf ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯ADIf ABCDEF is a regular hexagon , then
¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF =A4¯¯¯¯¯¯ADB3¯¯¯¯¯¯ADC2¯¯¯¯¯¯ADD¯¯¯¯¯¯AD
¯a=2¯i+¯j−2¯kand¯b=¯i+¯j if ¯c is a vector such that ¯a⋅¯c=|¯c|,|¯c−¯a|=2√2 and and the angle between¯aׯband¯c is 30∘, then ∣∣(¯aׯb)ׯc∣∣=
View SolutionThe value of a for which the angle between ¯a=2a2¯i+4a¯j+¯kand¯b=7¯i−2¯j+a¯k is obtuse and the angle between ¯b and z-axis is acute and less than π6 is
View SolutionIn the figure 11.34, ABCD is a quadrilateral in which ¯¯¯¯¯¯AB=¯¯¯¯¯¯ADand¯¯¯¯¯¯BC=¯¯¯¯¯¯DC. Diagonals ¯¯¯¯¯¯ACandBD intersect each other at O.Show that-
View SolutionABCDE is a regular hexagon. i) If ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED+¯¯¯¯¯¯AC=λ¯¯¯¯¯¯AC then λ=
View SolutionABC is an equilateral triangle. P and Q are two points on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯AC respectively such that ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯¯BC. If ¯¯¯¯¯¯PQ=5cm, then area of ΔAPQ is :
View Solution