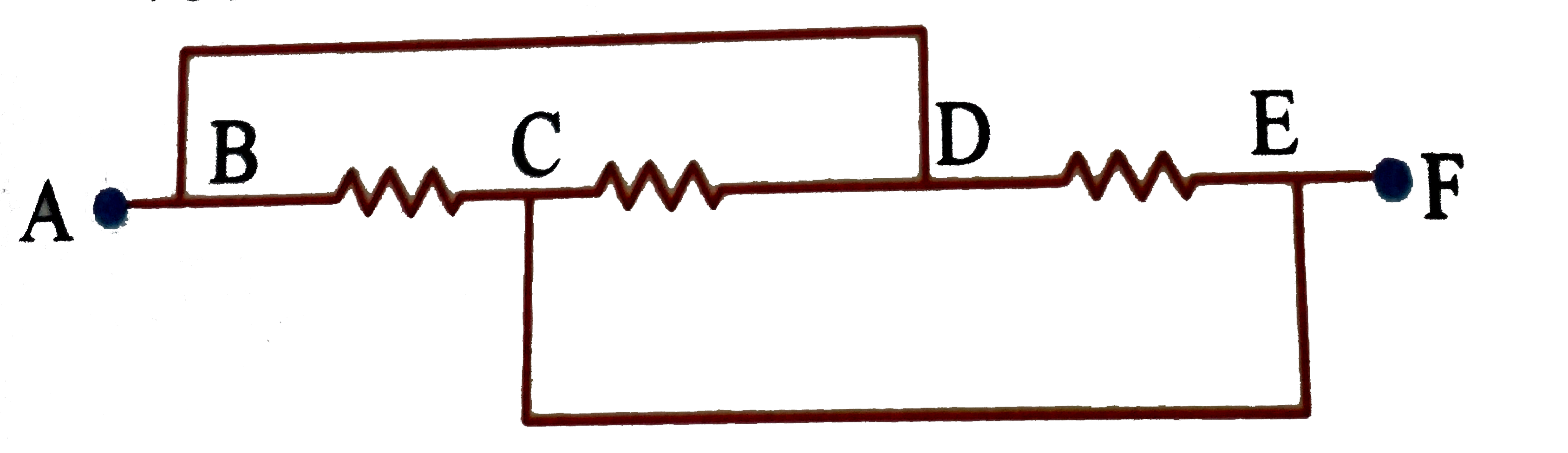
Three resistance each of are connected to form a triangle. The resistance between any two terminals is
The correct Answer is:D
To find the equivalent resistance between any two terminals of a triangle formed by three resistances of 4Ω each, we can follow these steps:
Step 1: Identify the Configuration
We have three resistors, each of resistance R=4Ω, connected in a triangular configuration. Let's label the vertices of the triangle as A, B, and C, with resistors as follows:
- RAB=4Ω (between A and B)
- RBC=4Ω (between B and C)
- RCA=4Ω (between C and A)
Step 2: Choose Two Terminals
We will calculate the equivalent resistance between terminals A and B.
Step 3: Analyze the Circuit
When looking at the resistors connected to terminals A and B:
- The resistor RAB is directly between A and B.
- The resistors RAC and RBC are connected in series between A and C and B and C, respectively.
Step 4: Calculate Total Resistance
1. Calculate the resistance of the two resistors RAC and RBC in series:
RAC+RBC=4Ω+4Ω=8Ω
2. Now, we have RAB (4 Ω) in parallel with the total resistance of RAC+RBC (8 Ω):
RAB (4 Ω) is in parallel with RAC+RBC (8 Ω)
3. Using the formula for resistors in parallel:
RAB=R1⋅R2R1+R2
where R1=4Ω and R2=8Ω:
RAB=4⋅84+8=3212=83Ω
Final Answer
The equivalent resistance between any two terminals (A and B) is:
RAB=83Ω
---
We have three resistors, each of resistance R=4Ω, connected in a triangular configuration. Let's label the vertices of the triangle as A, B, and C, with resistors as follows:
- RAB=4Ω (between A and B)
- RBC=4Ω (between B and C)
- RCA=4Ω (between C and A)
We will calculate the equivalent resistance between terminals A and B.
When looking at the resistors connected to terminals A and B:
- The resistor RAB is directly between A and B.
- The resistors RAC and RBC are connected in series between A and C and B and C, respectively.
1. Calculate the resistance of the two resistors RAC and RBC in series:
RAC+RBC=4Ω+4Ω=8Ω
RAB (4 Ω) is in parallel with RAC+RBC (8 Ω)
RAB=R1⋅R2R1+R2
where R1=4Ω and R2=8Ω:
RAB=4⋅84+8=3212=83Ω
The equivalent resistance between any two terminals (A and B) is:
RAB=83Ω
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three resistances of 2Ω each are connected in a triangle. The resistance in ohms between any two comers is
A3ΩB4ΩC6ΩD43ΩThree resistances of 2Ω each are connected in a triangle. The resistance in ohms between any two comers is
A3ΩB4ΩC6ΩD43ΩThree resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
A4/3 ohmB3/4 ohmC3 ohmD6 ohm
Three resistance of 12Ω are connected in the form of an equilateral triangle. The effective resistance between two corners, is
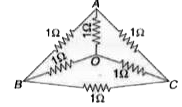
View SolutionSix equal resistances, each 1Ω, are joined to form a network as shown in fig. Then the resistance between any two corners is
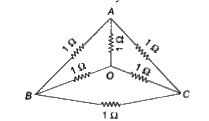
View SolutionSix equal resistances, each 1Ω, are joined to form a network as showing figure Then the resistance between any two corners is
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View SolutionA wire has resistance 12 ohms. If it is bent in the form of a equilateral triangle. The resistance between any two terminals in ohms is:
View Solution