Question

एक पत्थर एक मीनार की चोटी से क्षैतिज से कोण ${30}^{\circ }$ बनाता हुआ ऊपर की ओर वेग 16 मी/से से फेंका जाता है। फेंकने के 4 सेकण्ड पश्चात वह नीचे जमीन पर टकराता है। जमीन से मीनार की ऊँचाई तथा पत्थर की क्षैतिज परास ज्ञात कीजिए । पत्थर का मार्ग कैसा होगा ? $\left({\text{g = 9.8 मी/से}}^2\right)$

Explanation

पत्थर के प्रारम्भिक वेग u (= 16 मी/से) का क्षैतिज घटक
`u_(x)=u cos theta=16cos30^(@)=16xx(sqrt3//2)=8sqrt3` मी/से
तथा ऊर्ध्वाधर घटक `" "u_(y)=u sin theta=16 sin 30^(@)=16xx(1)/(2)=8` मीटर/सेकण्ड (ऊपर की ओर)।
ऊर्ध्वाधर वेग (ऊपर की ओर ) के कारण पत्थर कुछ ऊँचाई (माना y ) तक ऊपर जाएगा जब तक कि उसका अंतिम ऊर्ध्वाधर वेग शून्य न हो जाए ।माना इस गति में लगा समय t है, तो
समीकरण `v_(y)=u_(y)+a_(y)t` से (जँहा `a_(y)=-g` ),
`0=8-9.8t" या "t=8//9.8=0.816` सेकण्ड ।
इतना ही समय उसे उच्चतम बिंदु से वापस मीनार का चोटी के तल में स्थित बिंदु B तक आने में लगेगा । अतः बिंदु B के बाद पृथ्वी तल तक आने में लगा शेष समय `=4-(2xx0.816)=2.37` सेकण्ड।

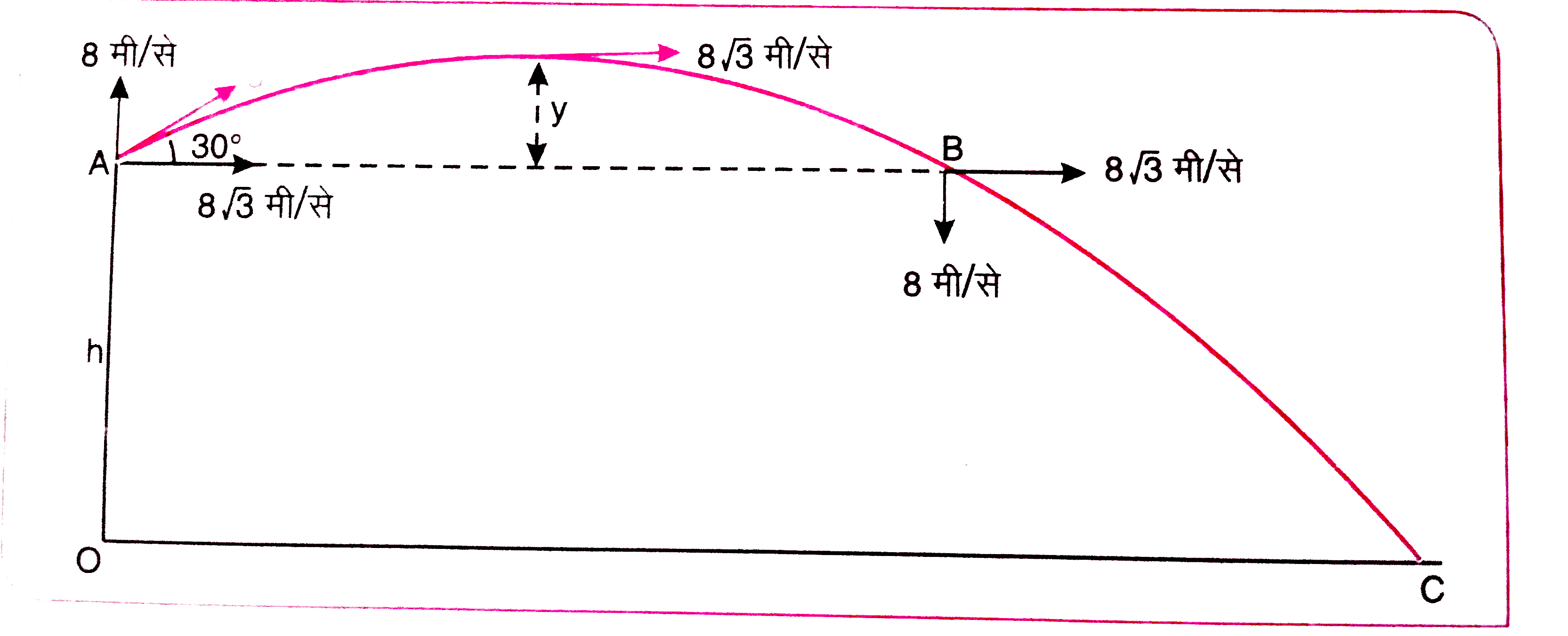
इतने समय (= 2.37 सेकण्ड) में पत्थर मीनार की ऊँचाई के बराबर ऊर्ध्वाधर दुरी नीचे की ओर तय करेगा। माना मीनार की ऊँचाई h है, तो सूत्र `y=u_(y)t+(1)/(2)a_(y)t^(2)` में `u_(y)=8` मी/से, `a_(y)=+g, t = 2.37` सेकण्ड तथा y = h रखने पर,
`h=8xx2.37+(1)/(2)xx9.8xx(2.37)^(2)=46.48` मीटर।
अर्थात जमीन से मीनार की ऊँचाई मीटर क्षैतिज दिशा में पत्थर का वेग नियत रहता है (अर्थात क्षैतिज दिशा में त्वरण `a_(x)=0` ), अतः पत्थर द्वारा t = 4 सेकण्ड में तय दुरी (या पत्थर की क्षैतिज परास) सूत्र `x=u_(x)t+(1)/(2)a_(x)t^(2)` से,
`OC=u_(x) xx t=8sqrt3xx4=55.4` मीटर ।