A conducting solid sphere having uniform charge Q on it has radius R. It is rotating with anangular velocity ω. If a uniform magnetic field B is present perpendicular to axis of rotation then the torque on sphere will be
qωR25B
qωR23R
qωR24B
qωR22R
The correct Answer is:B
Magnetic moment of sphere is M then
M23mR2ω=q2m
⇒M=qωR23
Torque =MBsin90∘=qωR2B2
Topper's Solved these Questions
Similar Questions
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
Knowledge Check
A conducting sphere of radius r has a charge . Then .
Athe charge is uniformly distributed over its surface if there is an external electric field .BDistribution of charge over its surface will be non uniform if no external electric field exist in space,CElectric field strength inside the sphere will be equal to zero only when no external electric field existsDPotential at every point of the sphere must be sameA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
 Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πR
Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πRA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
A(a) The emf will be maximum at the moment when flux is zeroB(b) The emf will be 0 at the moment when flux ismaximumC( c) The emf will be maximum at the moment when plane of the loop is parallel to the magnetic fieldD(d) The phase difference between the flux and the emf π/2
A conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA thin uniformring of radius R carrying uniform charge Q and mass M rotates about its axis with angular velocity ω. The ratio of its magnetic moment and angular momentum is:
View SolutionAn equilateral triangular conducting frame is rotated with angular velocity ω in a uniform magnetic field B as shown. Side of triangle is l. choose the correct options
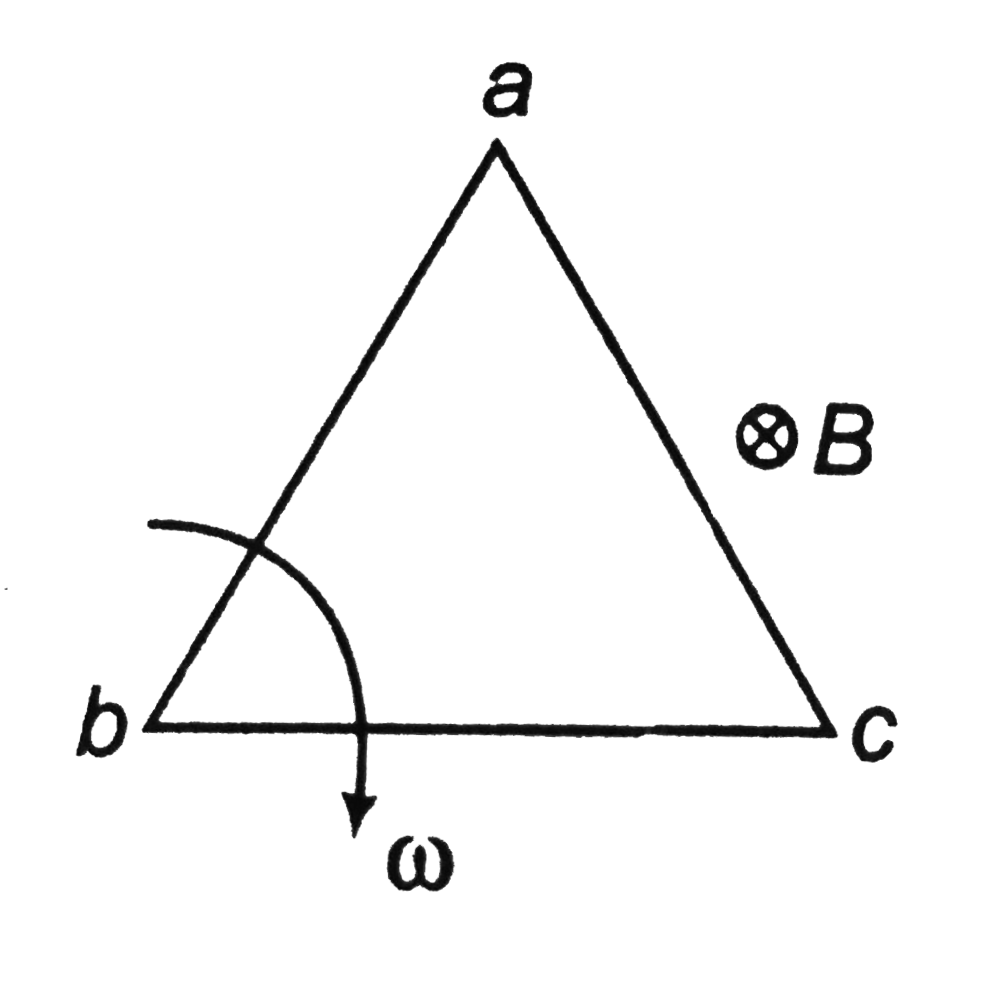
View SolutionThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is

View Solution
