The length of longest interval in which Roll's theorem can be applied for the function f(x)=∣∣x2−a2∣∣,(a>0) is:
A
2a
B
4a2
C
a√2
D
a
Text Solution
The correct Answer is:A
f(x)=∣∣(x2−a2)∣∣
f(x)=|(x−a)(x+a)|
plalting f(x), we can see that f is continous on [-a,a], differentiating on (-a,a) and also f(−a)=f(a), and there also exists a points C =0 in (-a,a) where f'( C)=0, so the length of the longest interval is 2a.
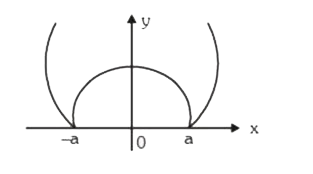
|
Similar Questions
Knowledge Check
Rolle's theorem is true for the function f(x)=x2−4 in the interval
A[−2,0]B[−2,2]C[0,12]D[0,2]The length of the longest interval in which the function f(x)=x3−3a2x+4 is decreasing is (∀a>0)
AaB2aC3aD4a
The length of the longest interval in which the function f(x)=x3−3a2x+4 is decreasing is (∀a>0)
View SolutionVerify Rolle's theorem for the function f(x)=x3−3x2+2x in the interval [0,2].
View SolutionVerify Rolle's theorem for the function f(x)=x3−3x2+2x in the interval [0,2].
View SolutionVerify Rolle's theorem for the function f(x)=x(2−x) in the interval [0,2]
View SolutionVerify the Rolle's theorem for the functionf(x)=x2−3x+2 on the interval [1,2].
View SolutionIs Rolle's Theorem applicable to the function:
f(x) = |x| in the interval [-1, 1]?
View Solution
