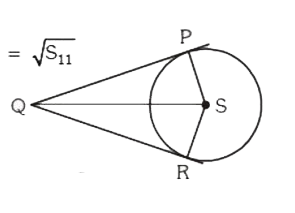
The area of the quadrilateral formed by the tangents from the point (4

If the area of a quadrilateral formed by the tangents from the origin to $x^{2} + y^{2} + 6 x - 10 y + λ = 0$ and the pair of radii at the points of contact of these tangents to the circle, is 8 $c m^{2}$ , then the value of $λ$ must be
A2
B4
C16
D32
A circle $C_{1}$ of radius 2 units rolls o the outerside of the circle $C_{2} : x^{2} + y^{2} + 4 x = 0$ touching it externally.
Area of a quadrilateral found by a pair of tangents from a point of $x^{2} + y^{2} + 4 x - 12 = 0$ to $C_{2}$ with a pair of radii at the points of contact of the tangents is ( in sq. units )
A $2 \sqrt{3}$
B $4 \sqrt{3}$
C $\sqrt{3}$
D $3 \sqrt{3}$
The area of the triangle formed by the tangents from the point (4,3) to the circle $x^{2} + y^{2} = 9$ and the line joining their points of contact in sq. units is
A $\frac{132}{25}$
B $\frac{162}{25}$
C $\frac{192}{25}$
Dnone

The area of the quadrilateral formed by the tangents from the point (4,5) to the circle $x^{2} + y^{2} - 4 x - 2 y - 11 = 0$ with the pair of radii through the points of contact of the tangents is: