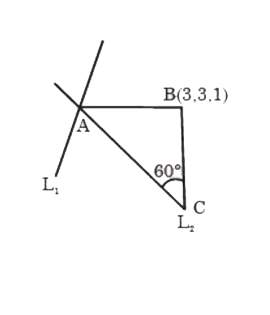
Let L1:→r=(→i+→j+→k)+λ(→i+→j),λ∈R,L2:ˆi+(μ+1)ˆj+(μ+1)ˆk,μ∈R are two lines intersecting at point 'A'. Through point B(3,3,1) a line in drawn making an angle of 60∘ with L2 and intersecting it a point 'C'. Then area of △ABC is:
2√2
3√2
2√3
3√3
The correct Answer is:C
→r=(111)+λ(110)
r=(1,1,1)+μ(0,1,1)
int pt. A≡(1,1,1)
Let c be (1,1+μ,1+μ)
−−→AC=011
−−→BC=2,2−μ,−μ
ACBC=60∘⇒0+2−μ−μ√2√4+(2−μ)2+μ2=12
(4+4μ)2=2(4+4+μ2−4μ+μ2)
16(1+μ2−2μ)=(16+4μ2−8μ)
12μ2−24μ⇒μ=0,μ=2
μ=0,μ=2
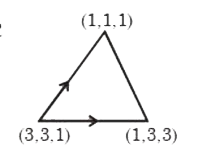
C(1,1,1)(1,3,3)
12∣∣
∣
∣∣ˆiˆjˆk−202−2−20∣∣
∣
∣∣=12{ˆi(4)−ˆj(4)+k(4)}
∣∣(2ˆi−2ˆj+2ˆk)∣∣=2√3=a√b
a=2, b=3
Similar Questions
Let a place P contain two lines
→r=ˆi+λ(ˆi+ˆj),λ∈R and
→r=−ˆj+μ(ˆj−ˆk),μ∈R .
If Q(α,β,γ) is the food of the perpendicular drawn from the point M(1,0,1) to P, then 3(α+β+γ) equals ____________.View SolutionShow that the lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj) and →r=4ˆi+ˆk+μ(2ˆi+3ˆk) intersect. Also find the co[-ordinates of their point of intersection.
View Solution
Knowledge Check
- Question 1 - Select One
Consider a plane ∏:→r⋅(2ˆi+ˆj−ˆk)=5, a line L1:→r=(3ˆi−ˆj+2ˆk)+λ(2ˆi−3ˆj−ˆk) and a point a(3,−4,1)⋅L2 is a line passing through A intersecting L1 and parallel to plane ∏.
Q. Line L1 intersects plane ∏ at Q and xy-plane at R the volume of tetrahedron OAQR is :
(where 'O' is origin)A0B143C37D73 - Question 2 - Select One
Consider a plane ∏:→r⋅(2ˆi+ˆj−ˆk)=5, a line L1:→r=(3ˆi−ˆj+2ˆk)+λ(2ˆi−3ˆj−ˆk) and a point a(3,−4,1)⋅L2 is a line passing through A intersecting L1 and parallel to plane ∏.
Q. Line L1 intersects plane ∏ at Q and xy-plane at R the volume of tetrahedron OAQR is :
(where 'O' is origin)A0B143C37D73
If →r=(ˆi+2ˆj+3ˆk)+λ(ˆi−ˆj+ˆk) and →r=(ˆi+2ˆj+3ˆk)+μ(ˆi+ˆj−ˆk) are two lines, then the equation of acute angle bisector of two lines is
View SolutionShow that the lines :
→r=3ˆi+2ˆj−4ˆk+λ(ˆi+2ˆj+2ˆk)
and →r=5ˆi−2ˆj+μ(3ˆi+2ˆj+6ˆk)
(ii) →r=(ˆi+ˆj−ˆk)+λ(3ˆi−ˆj).
and →r=(4ˆi−ˆk)+μ(2ˆi+3ˆk)
are intersecting. Hence, find their point of intersection.View SolutionDetermine whether or not the following pairs of lines intersect :
→r=(2λ+1)ˆi−(λ+1)ˆj+(λ+1)ˆk.
and →r=(3μ+2)ˆi−(5μ+5)ˆj+(2μ−1)ˆk.View SolutionConsider a plane ∏:→r⋅(2ˆi+ˆj−ˆk)=5, a line L1:→r=(3ˆi−ˆj+2ˆk)+k(2ˆi−3ˆj−ˆk) and a point A(3,−4,1)⋅L2 is a line passing through A intersecting L1 and parallel to plane ∏.
Q. Line L1 intersects plane ∏ at Q and xy-plane at R the volume of tetrahedron OAQR is :
(where 'O' is origin)View SolutionIf the lines →r=(2→i)+λ(→i+2→j+m→k) and →r=(→i+→j)+μ(2→i+→j+2vcek) are perpendicular to each other, then m=
View SolutionFind the shortest distance between the following (1-4) lines whose vector equations are :
(i) →r=(λ−1)ˆi+(λ−1)ˆj−(1+λ)ˆk
and →r=(1−μ)ˆi+(2μ−1)ˆj+(μ+2)ˆk
(ii) →r=(1+λ)ˆi+(2−λ)ˆj+(1+λ)ˆk
and →r=2(1+μ)ˆi−(1−μ)ˆj+(−1+2μ)ˆk .View Solution

