Let 'A' be the area bounded by the curves
y2=4k1x,k1∈[18,14]
x2=4k2(2−y),k2∈[14,1] and y-axis in the first quadrant. Then the least value of A is
Text Solution
The correct Answer is:A
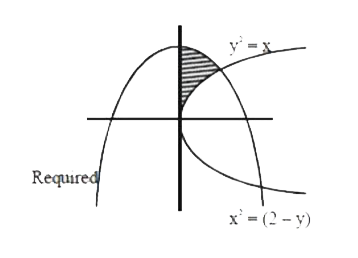
Required
A=∫10(2−x2−√x)dx
=2−13−23=2−1=1
|
Similar Questions
Knowledge Check
Let A(k) be the area bounded by the curves y=x2+2x−3andy=kx+1. Then
Athe value of k for which A(k) is least is 2Bthe value of k for which A(k) is least is 3/2Cleast value of A(k) is 32/3Dleast value of A(k) is 64/3The area bounded by the curves y=(x−1)2,y=(x+1)2 and y=14 is
A13 sq unitB23 sq unitC14 sq unitD15 sq unitThe area bounded by the curves y=(x−1)2,y=(x+1)2 and y=14 is
A1/6B2/3C1/4D1/3
The area bounded by the curves y=(x−1)2,y=(x+1)2 and y=14 is
View SolutionFind the area bounded by the curve y=4x2,x=0,x=1 and y=4 in first quadrant.
View SolutionConsider the curves
C1:y2=4k1x∀k1∈[18,14]
C2:x2=4k2(y−2)∀k2∈[−1,−14]
C3:x=0
Then minimum area bounded by all of these three curves is
View SolutionThe area bounded by the curve y=x2+2x+1 and tangent at (1,4) and y -axis is
View SolutionThe area bounded by the curve y=x2+2x+1, the tangent at (1,4) and the y-axis is
View Solution
