The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4 x - 5 y = 20$ to the circle $x^{2} + y^{2} = 9$ is :

A

$20 (x^{2} + y^{2}) - 36 x + 45 y = 0$

B

$20 (x^{2} + y^{2}) + 36 x - 45 y = 0$

C

$36 (x^{2} + y^{2}) - 20 x + 45 y = 0$

D

$36 (x^{2} + y^{2}) + 20 x - 45 y = 0$

Text Solution

Verified by Experts

The correct Answer is:A

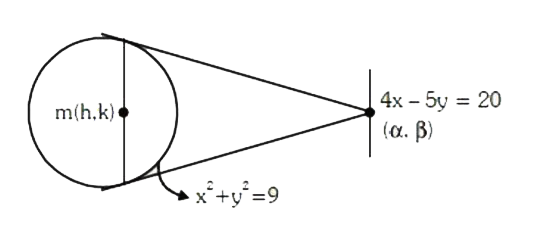
$T = S_{1}$
$x h + y k - 9 = h^{2} + k^{2} - 9$
$x h + y k = h^{2} + k^{2}$ ……(1)
$4 α - 5 b a t a = 20$ ……(2)
equation of COC
T = 0
$x α + y β = 9$ ………(3)
Eq. (1) & (3)
$\frac{h}{α} = \frac{k}{β} = \frac{h^{2} + k^{2}}{9}$
or $\frac{9 h}{h^{2} + k^{2}}, β = \frac{9 k}{h^{2} + k^{2}}$
Put in equation (2)
$20 (x^{2} + y^{2}) - 36 x + 45 y = 0$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
The chords of contact of the pair of tangents drawn from each point on the line $2 x + y = 4$ to the circle $x^{2} + y^{2} = 1$ pass through the point
A $(1, 2)$
B $(\frac{1}{2}, \frac{1}{4})$
C(2, 4)
Dnone
Question 2 - Select One
The chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle $x^{2} + y^{2} = 1$ pass through a fixed point
A(2,4)
B(-1/2,-1/4)
C(1/2,1/4)
D(-2,-4)

Recommended Questions

Home
Ask Doubt
Profile