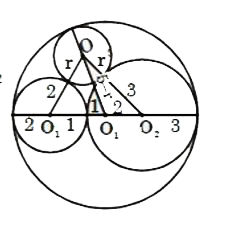
If S,S1,S2 be the circles of radii 5, 3, 2 respectively. If S1 and S2 touch externally and they touch internally with S. The radius of circle S3 which touches externally with S1 and S2 and internally with S is :
3019
127
54
Can't be determined
The correct Answer is:A
For diagram we get
(r+2)2+(r+3)23
=2.32+3.22+5(5−r)2
⇒76r=120
⇒r=12076
⇒r=3019
Similar Questions
Let S1 and S2 denote the circles x2+y2+10x−24y−87=0 and x2+y2−10x−24y+153=0 respectively. The value of a for which the line y=ax contains the centre of a circle which touches S2 externally and S1 internally is
View SolutionLet S1:x2+y2=9andS2:(x−2)2+y2=1. Then the locus of centre of a variable circle S which touches S1 internally and S2 externally always passes through the points:
View Solution
Knowledge Check
If S1,S2,S3 are the sums of n, 2n, 3n terms respectively of an A.P., then S3/(S2−S1)−
A1B2C3D4The equation (s) of circle (s) touching 12x−5y=7 at (1, 1) and having radius 13 is/are
Ax2+y2−22x+12y−1=0Bx2+y2+22x−12y−12=0Cx2+y2−26x−8y+16=0Dx2+y2−26x+8y+16=0
If two circles S=0 and s'=0 are touch each other externally then
View SolutionThe equation (s) of circle (s) touching 12x−5y=7 at (1, 1) and having radius 13 is/are
View SolutionIf S1,S2,S3 are the sums to n, 2n, 3n terms respectively for a GP then prove that S1,S2−S1,S3−S2 are in GP.
View SolutionLet S1andS2 be circle passing through (2,3) and touching the coordinate acea and S be the circle having common points of S1andS2 as the centre and radius equal to G.M of radius of S1andS2 then
View SolutionLet S1andS2 be circle passing through (2, 3) and touching the coordinate axis and S be the circle having common points of S1andS2 as the centre and radius equal to G.M of radius of S1andS2 then
View SolutionIf s1,s2ands3 are the sum of first n , 2n, 3n terms respectively of an arithmetical progression , then show that s3=3(s2−s1)
View Solution
