The triangle of maximum area inscribed in a circle is :

A

equilateral

B

isosceles

C

right-angled

D

none of these

Text Solution

Verified by Experts

The correct Answer is:A

The area of the triangle is maximum, when vertex C is at maximum distance from the base AB, or C is a point on diameter perpendicular to AO, OC = OB = a.
$∴ Δ A B C$ is isosceles triangle.

Area of $Δ A B C$ is $z = \frac{1}{2} \times A B \times C D$
$= a^{2} \sin 2 θ (1 + \cos 2 θ)$
$∴ \frac{d z}{d θ} = 2 a^{2} (\cos 4 θ + \cos 2 θ) = 0$
$\Rightarrow 2 \cos 3 θ \cos θ = 0$
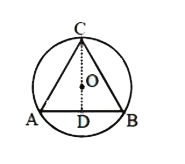
$\Rightarrow θ = \frac{π}{2}$ or $θ = \frac{π}{6}$
$∴ θ = \frac{π}{2}$ is impossible,
$∴$ at $θ = \frac{π}{6}$ area of triangle is maximum.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
If a triangle of maximum area is inscribed within a circle of radius R, then

A $S = 2 R^{2}$
B $\frac{1}{r_{1}} + \frac{1}{r_{2}} + \frac{1}{r_{3}} = \frac{\sqrt{2} + 1}{R}$
C $r = (\sqrt{2} - 1) R$
D $s = (1 + \sqrt{2}) .2 R$
Question 2 - Select One
If a triangle of maximum area is inscribed within a circle of radius R, then

A $S = 2 R^{2}$
B $\frac{1}{r_{1}} + \frac{1}{r_{2}} + \frac{1}{r_{3}} = \frac{\sqrt{2} + 1}{R}$
C $r = (\sqrt{2} - 1) R$
D $s = (1 + \sqrt{2}) .2 R$
Question 3 - Select One
If a right angled triangle ABC of maximum $Δ$ area is inscribed in a circle of radius R , then
A $Δ = 2 R^{2}$
B $r = (\sqrt{2} - 1) R$
C $\frac{1}{r_{1}} + \frac{1}{r_{2}} + \frac{1}{r_{3}} = \frac{\sqrt{2} - 1}{R}$
D $s = (\sqrt{2} - 1) R$

Recommended Questions

Home
Ask Doubt
Profile