If maximum & minimum value of function f(x)=x3−6x2+9x+1∀x∈[0,2] are M & m respectively, then value of M–2m is :
Video Solution
Text Solution
The correct Answer is:3.00
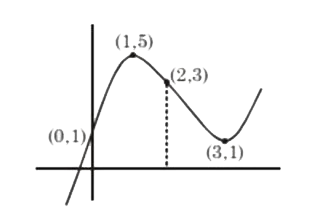
∴M=5 and m = 1
M−2m=3
|
Similar Questions
Knowledge Check
The minimum value of the function f(x)=x3−3x2−9x+5 is :
A−9B10C3D16Minimum value of f(x)=6x3−9x2−36x+24 is
A36B−72C−36D72The minimum value of the function f(x)=tanx3+2tanx,∀x∈[0,π2) is
A0B12C13D16
Let M and m respectively be the maximum and minimum values of the function
f(x)=tan−1(sinx+cosx) in [0,π2]. Then the vlaue of tan(M−m) is equal to :
View SolutionLet minimum and maximum value of y=2x3−15x2−36x+1∀x∈[0,3] is m and M. Then
View SolutionFind the maximum and minimum values of the following functions.
f(x)=x3−2x2+x+6
View SolutionThe difference between the maximum and minimum values of the function f(x)=x3−3x+4,∀x∈{0,1] is
View SolutionReal number x,y satisfies x2+y2=1. If the maximum and minimum value of the expression z=4−y7−x are Mandm respectively, then find the value (2M+6m).
View Solution
