A resistance R2 is connected in parallel with a resistance R1 what resistance R3 must be connected in series with the combination of R1andR2 so that the equivalent resistance is equal to the resistance R1 -
R21R1+R2
(R1+R2)2R1
R22R1+R2
R21R2
The correct Answer is:A
Accordingly R1R2R1+R2+R3=R1
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Resistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
An2RBR/n2CR/nDnR - Question 2 - Select One
R is the equivalent resistance of n resistors of same resistance in series. If the connection is turned parallel then equivalent resistance will be:
An2RBnRCRnDRn2 - Question 3 - Select One
If a resistanceR2 is connected in parallel with the resistance R in the circuit shown, then possible value of current through R and the possible value of R2 will be
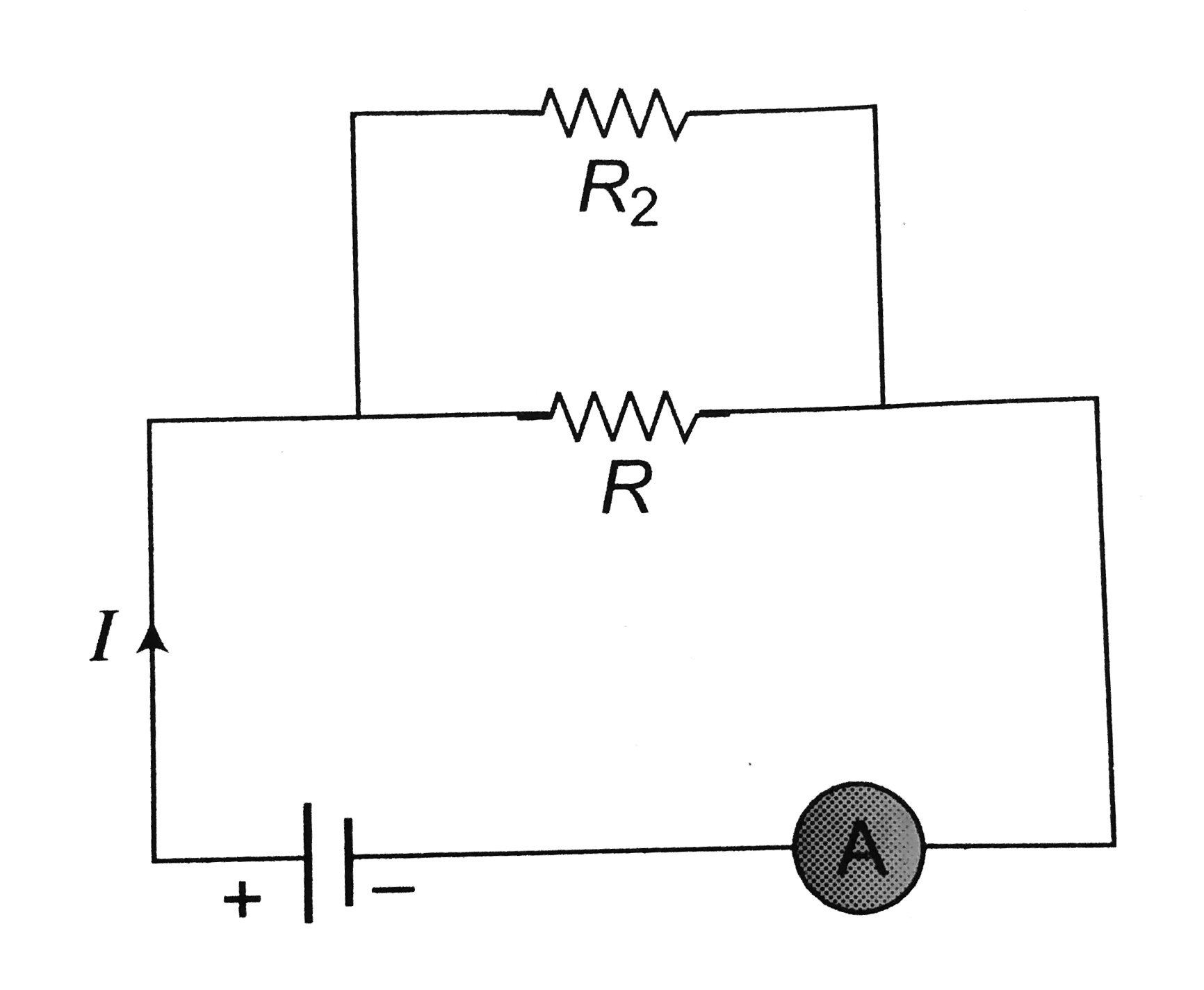 AI3,RBI.2RCI3,2RDI2,R
AI3,RBI.2RCI3,2RDI2,R
Two conductors of resistance R1(50±2) ohm and R2=(100±4) ohm are connected in (a) series and (b) parallel. Find the equivalent resistance.
View SolutionTwo resistance R1=100±3ΩandR2=200±4Ω are connected in seriesg. What is their equivalent resistance?
View SolutionA galvanometer of resistance G is converted into a voltmenter to measrue upto V volts by connecting a resistance R1 in series with the coil. If a resistance R2 is connected series with it, then it can measure upto 1//2 volts. Find the resistance, in terms of R1 and R2, required to be connected to convert in into a voltmeter that can read upto 2V. Also find the resistance G of the galvanometer in terms of R1 and R2
View SolutionA resistance R1 is connected to a source of constant voltage . On connecting a resistance R2 in series with R1
View SolutionA coil of some internal resistance 'r' behaves line an inductance. When it is connected in series with a resistance R1, the time constant is found to be τ1. When it is connected in series with a resistance R2, the time constant is found to be τ2. The inductance of the coil is
View Solution

