Two bodies of different masses ma and mb are dropped from two different heights a and b. The ratio of the time taken by the two to cover these distances are
a: b
b :a
√a:√b
a2:b2
The correct Answer is:C
To solve the problem of finding the ratio of the time taken by two bodies of different masses dropped from different heights, we can follow these steps:
1. Understanding the Problem:
We have two bodies with masses ma and mb dropped from heights A and B respectively. We need to find the ratio of the time taken by each body to reach the ground.
2. Acceleration Due to Gravity:
Both bodies experience the same acceleration due to gravity g since the mass of the objects does not affect the time taken to fall in a vacuum.
3. Using the Equation of Motion:
We can use the second equation of motion:
s=ut+12at2
where s is the distance fallen, u is the initial velocity, a is the acceleration, and t is the time taken.
4. Initial Conditions:
Since both bodies are dropped (not thrown), their initial velocity u=0. Thus, the equation simplifies to:
s=12gt2
5. For Body A:
For the body dropped from height A:
A=12gt21
Rearranging gives:
t21=2Ag(Equation 1)
6. For Body B:
For the body dropped from height B:
B=12gt22
Rearranging gives:
t22=2Bg(Equation 2)
7. Finding the Ratio of Times:
Now, we can find the ratio of the squares of the times:
t21t22=2Ag2Bg=AB
8. Taking the Square Root:
Taking the square root of both sides gives:
t1t2=√AB
9. Final Result:
Thus, the ratio of the time taken by the two bodies is:
t1t2=√AB
We have two bodies with masses ma and mb dropped from heights A and B respectively. We need to find the ratio of the time taken by each body to reach the ground.
Both bodies experience the same acceleration due to gravity g since the mass of the objects does not affect the time taken to fall in a vacuum.
We can use the second equation of motion:
s=ut+12at2
where s is the distance fallen, u is the initial velocity, a is the acceleration, and t is the time taken.
Since both bodies are dropped (not thrown), their initial velocity u=0. Thus, the equation simplifies to:
s=12gt2
For the body dropped from height A:
A=12gt21
Rearranging gives:
t21=2Ag(Equation 1)
For the body dropped from height B:
B=12gt22
Rearranging gives:
t22=2Bg(Equation 2)
Now, we can find the ratio of the squares of the times:
t21t22=2Ag2Bg=AB
Taking the square root of both sides gives:
t1t2=√AB
Thus, the ratio of the time taken by the two bodies is:
t1t2=√AB
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Critical Thinking
19 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Graphical Questions
23 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Relative Motion
13 Videos
- GRAVITATIONBOOK - ERRORLESS CHAPTER - GRAVITATIONEXERCISE - SET
27 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
Similar Questions
Ratio of speeds of A and B is a:b: then ratio of the time taken by them to cover the same distance
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
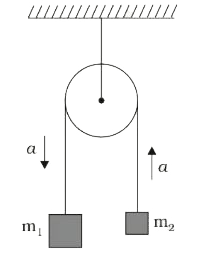
View Solution
Knowledge Check
Two bodies of different masses ma and mb are dropped from two different heights, viz, a and b. The ratio of time taken by the two to drop through these distance is:
Aa:bBma/mb:b/aC√a:√bDa2:b2Two bodies of different masses ma and mb are dropped from two different heights, viz, a and b. The ratio of time taken by the two to drop through these distance is:
Aa:bBmamb:baC√a:√bDa1:b2Two bodies of different masses are dropped from height of 16 m and 25 m respectively. The ratio of the times taken by them is
A2516B1625C54D45
Two bodies A (of mass 1 kg ) and B (of mass 3kg ) are dropped from heights of 16m and 25m ,respectively What is the ratio of the times taken by them to reach the ground?
View SolutionTwo objects are dropped together from the height h1 and h2 . The ratio of time taken by them to reach the earth is
View SolutionTwo bodies of masses m1 and m2(m1=2m2) are dropped from a height. The ratio of time taken by them to reach the ground is ________.
View SolutionTwo balls are dropped from heights h and 2h respectively. The ratio of time taken by these balls to reach the earth is
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View Solution
