Three capacitors A,B,C are connected in such a way that their equivalent capacitance is equal to the capacitance of B. The capacitances of A and B are 10μF and 30μF respectively and C≠0. Determine three possible values of C and also show how the capacitors are to be connected in the three cases.
Text Solution
The capacitor B cannot be joined in parallel to any combination of the capacitors A and C because in that case equivalent capacitance will be greater than the capacitance of B. The following three combination are possible.
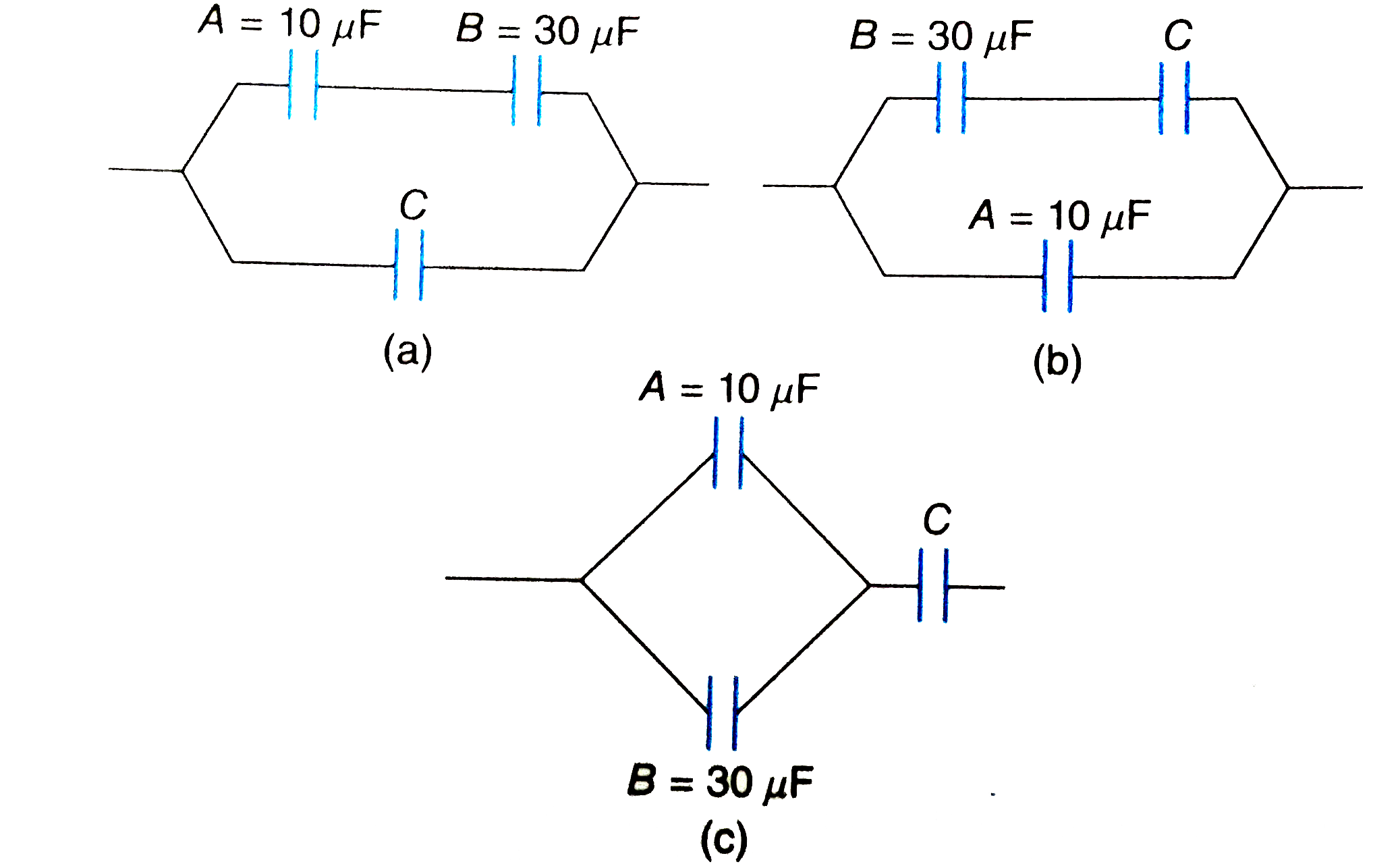
i) A and B are connected in series. Now C is connected in parallel with the series combination of A and B. According to the question,
10×3010+30+C=30 or, 30040+C=30
or, C=22.5μF
ii) B and C are connected in series. Now A is connected in parallel with the series combination of B and C. According to the question,
30×C30+C+10=30 or, 30×C30+C=20
or, C60μF
iii) A and B are connected in parallel. Now C is connedted in series with the parallel combination of A and B. According to the question,
40×C40+C=30 or 3(40+C)=4C or C=120μF.
|
Topper's Solved these Questions
- CAPACITANCE AND CAPACITORBOOK - CHHAYA PUBLICATIONCHAPTER - CAPACITANCE AND CAPACITOREXERCISE - SECTION RELATED QUESTIONS
30 Videos
- CAPACITANCE AND CAPACITORBOOK - CHHAYA PUBLICATIONCHAPTER - CAPACITANCE AND CAPACITOREXERCISE - HIGHER ORDER THINKING SKILL
39 Videos
- ATOMIC NUCLEUSBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMIC NUCLEUSEXERCISE - CBSE SCANNER
14 Videos
- COMMUNICATION STSTEMBOOK - CHHAYA PUBLICATIONCHAPTER - COMMUNICATION STSTEMEXERCISE - CBSE SCANNER
28 Videos
Similar Questions
Knowledge Check
Seven capacitor are connected as shown in the figure.
 .
.
The equivalent capacitance in μF between A and B is.A3.75B8.5C10.25D15Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
AConnecting them in parallelBConnecting two in series and one in parallelCConnecting two in parallel and one in seriesDConnecting all of them in seriesThree capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
Aconnecting them in seriesBconnecting them is parallelCconnecting two in series and one in parallelDconnecting two in parallel and one is series
Three capacitors 2μF,2μFand6μF are joined in series with each other.
The equivalent capacitance is-
View SolutionSix identical capacitors are connected as shown in figure. Capacitance of each capacitors is 5μF The effective capacitance between point A and B is
View SolutionThree capacitors Catcb<Cc are connected in series. Their resultant capacitance will be
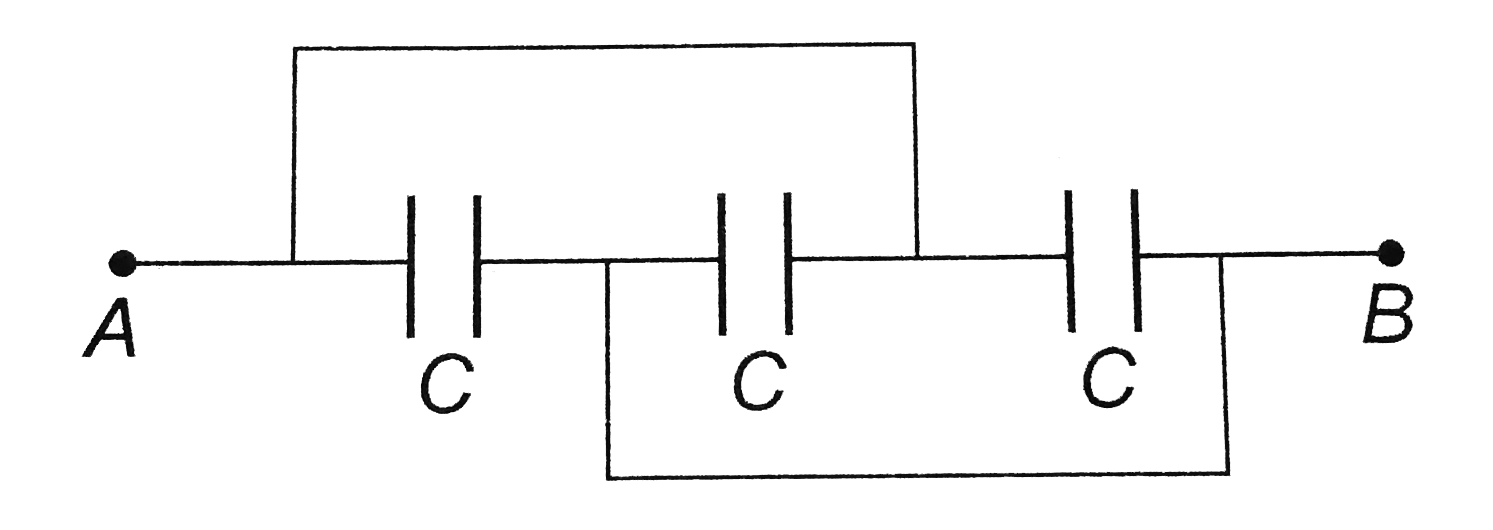
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
View SolutionThree capacitors 2μF,3,μFand6μF are joined'in series with each other.
The equivalent capacitance is:
View Solution

