Consider the circuit show in the figure . The value of the resistance X for which the thermal power gernerated in it is practically independent of small variation of its resistance is

X = R
X=R3
X=R2
X=2R
The correct Answer is:C
i=E(R+RXR+X)
[ I = main current in the circuit ]
VRX=ERXR+X(R+RXR+X)=EX(R+2X)
[potential differnce across two terminals of R and X]
PX=V2RXX=E2X(R+2X)2 [power consumed by X ]
∴dPXdX=E2(R−2X)(R+2X)3 or , dPX=E2(R−2X)(R+2X)3dX
Now if X=R2 , then for any value of dX , dPX=0
Topper's Solved these Questions
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - EXAMINATION ARCHIVE (JEE Main )
1 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - EXAMINATION ARCHIVE (AIPMT)
1 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - EXAMINATION ARCHIVE (WBCHSE)
3 Videos
- DIGITAL CIRCUITS BOOK - CHHAYA PUBLICATIONCHAPTER - DIGITAL CIRCUITS EXERCISE - CBSE SCANNER
6 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A circuit shown in the figure has resistances 20Ω and 30Ω. At what value of resistance Rx will the thermal power generated in it be practically independent of small variations of that resistance? The voltage between points A and B is supposed to be constant in this case.
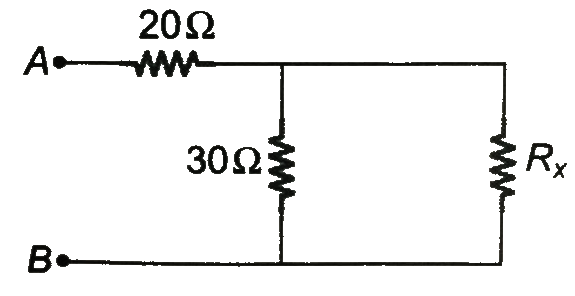
View SolutionA circuit shown in the figure has resistances 20Ω and 30Ω. At what value of resistance Rx will the thermal power generated in it be practically independent of small variations of that resistance? The voltage between points A and B is supposed to be constant in this case.

View Solution
Knowledge Check
Consider the circuit shown in the figure. The value of the resistance X for which the thermal power generated in it is practically independent of small variation of its resistance is
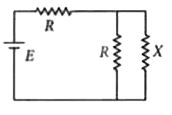 AX=RBX=R3CX=R2Dx=2R
AX=RBX=R3CX=R2Dx=2RConsider the circuit as shown in figure. The equivalent resistance between A and B is
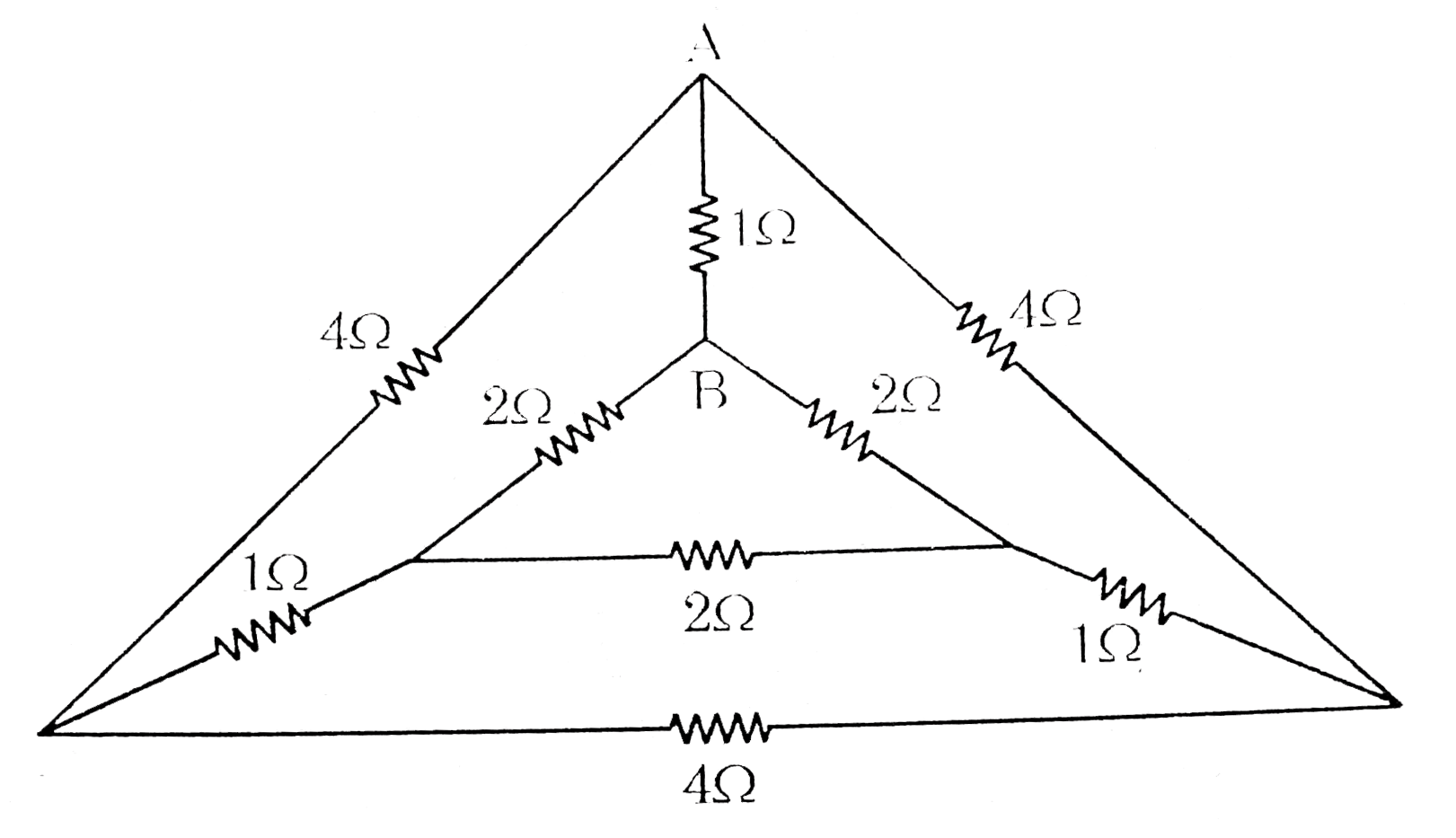 A97ΩB19ΩC79ΩDNone
A97ΩB19ΩC79ΩDNoneIn the circuit shown, the galvanometer shows zero current. The value of resistance R is :
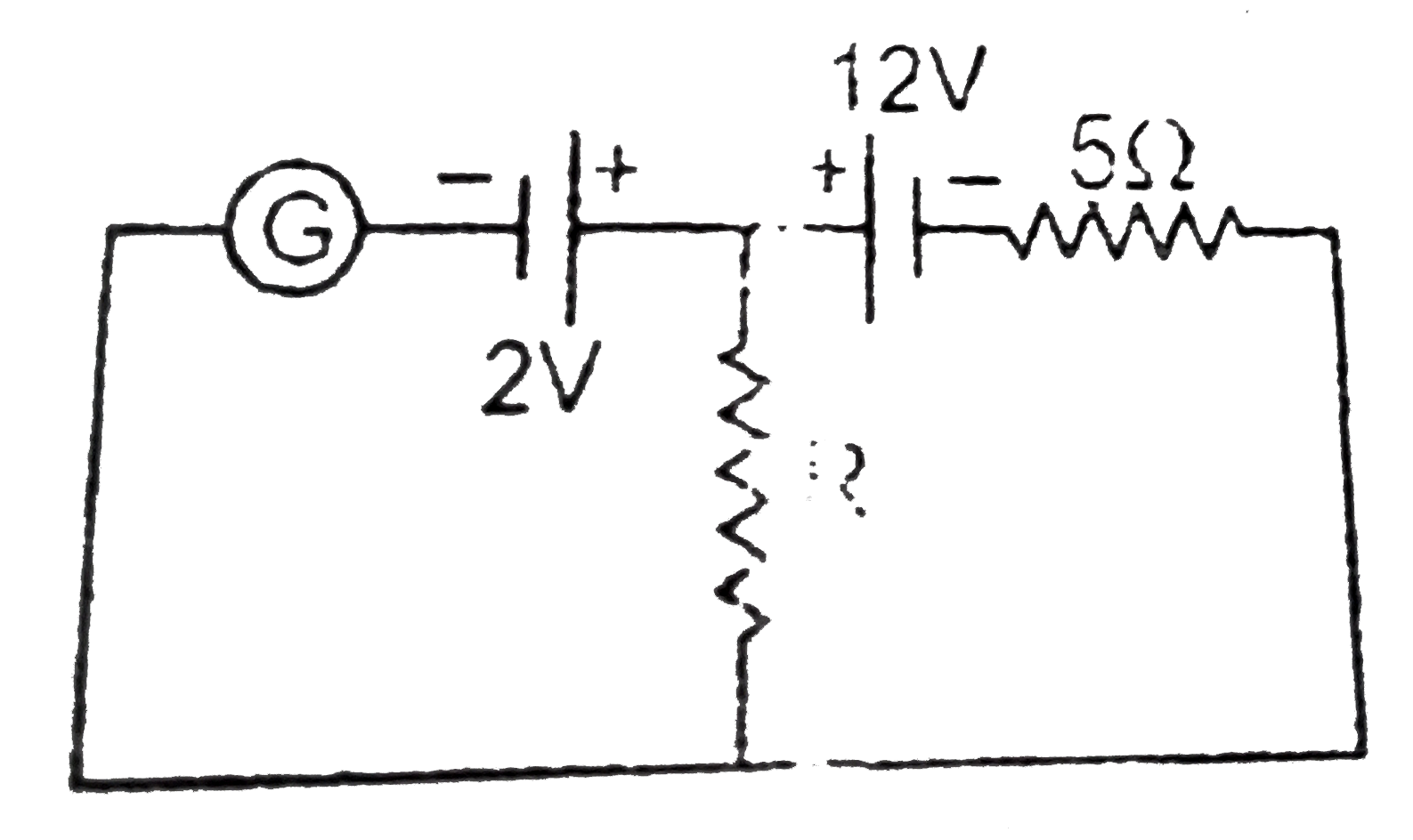 A1ΩB2ΩC4ΩD9Ω
A1ΩB2ΩC4ΩD9Ω
A circuit shown in Fig, has resistances R1=20Ω and R2=30Ω. At what value of the resitanace Rx will the thermal power generated in it practically independent of small variations of that resistance? The voltage between the points A and B is supposed to be constant in this case
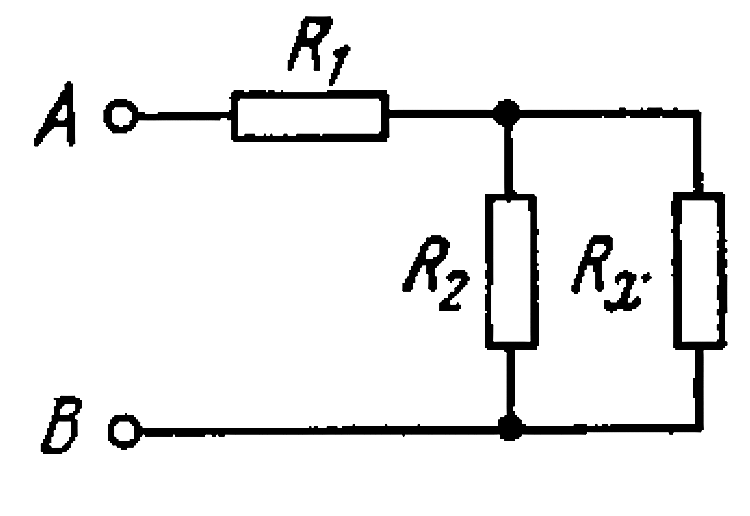
View SolutionConsider the circuit as shown in figure. The equivalent resistance between A and B is

View SolutionIn the circuit shown in figure-3.196, find the value of resistance ?R at which the power transferred to this resistance will be maximum.
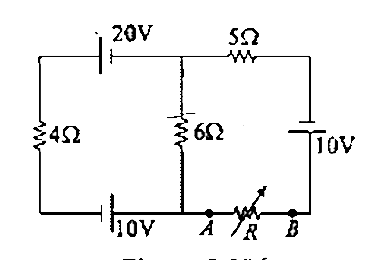
View SolutionIn the circuit shown, the galvanometer shows zero current. The value of resistance R is :

View SolutionIn the circuit shown, the galvanometer shows zero current. The value of resistance R is :

View Solution
