A current I is flowing through an infinitely long wire PQRS [Fig. 1.30]. The wire is bent at right angles so that the part QR becomes one-fourth of the circumference of a circle or radius r whose centre is at O. Determine the magnetic field at O.
![A current I is flowing through an infinitely long wire PQRS [Fig. 1.30]. The wire is bent at right angles so that the part QR becomes one-fourth of the circumference of a circle or radius r whose centre is at O. Determine the magnetic field at O.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CHY_DMB_PHY_XII_P1_U03_C01_SLV_007_Q01.png)
With respect to the point O, both the parts PQ and RS are semi-infinite wires and hence, for watch part magnetic field at the point O will be,
B1=B2=μ04π⋅Ir
Again for a complete circular conductor, the magnetic field at its centre =μ0I2r
So, for the one-fourth part QR of the circle, the magnetic field at O,
B3=14×μ0I2r=μ0I8r
Hence, the resultant magnetic field at O,
B=B1+B2+B3
=μ0I4πr+μ0I4πr+μ0I8r
=μ0I4r(1π+1π+12)=μ0(4+π)I8πr
Topper's Solved these Questions
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - SECTION RELATED QUESTIONS
64 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
48 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
- ELEMENTARY PHENOMENA OF ELECTROSTATICS BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE
2 Videos
Similar Questions
A current I flows through an infinitly long wire having infinite brands as shown. The radius of the first curved section is a and the radii of the successive curved portions each increases by a factor η. Find magnetic field at O.

View SolutionA current of I ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field at O is
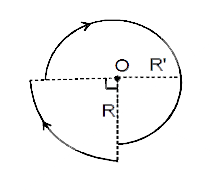
View Solution
Knowledge Check
1A current flows through an infinitely long straight wire. The magnetic field produced at a point 1 metres away from it is
A2×10−3 TeslaB210 TeslaC2×10−7 TeslaD2π×10−6 TeslaA current I=IA flowing through an infinite long wire A1 divides between two infinite long wires A2 and A3 at junction B. The magnitude of the magnetic field at point O due to current through wires is :
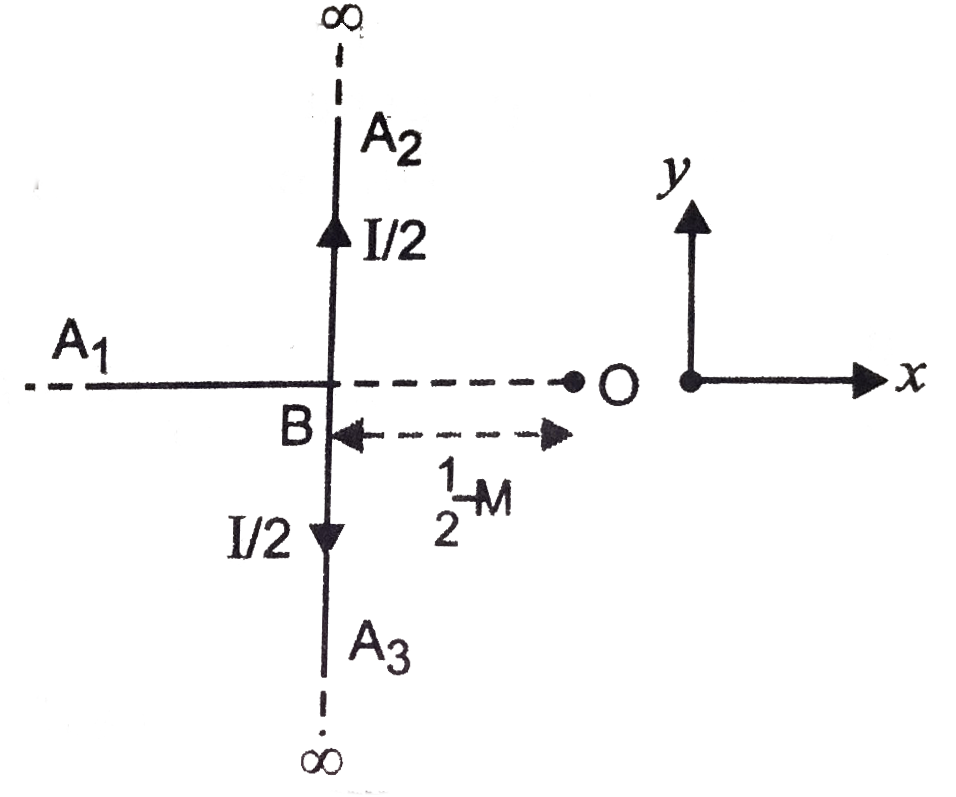 AzeroB2×10−7TC4×10−7TD8×10−7T
AzeroB2×10−7TC4×10−7TD8×10−7T
A current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
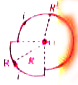
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionTwo very long wires carrying equal current i are bent and arranged as shown in figure. Both AB and CD are arcs of the same circle, both subtending right angles at the centre O. The magnetic field at O is:

View Solution
