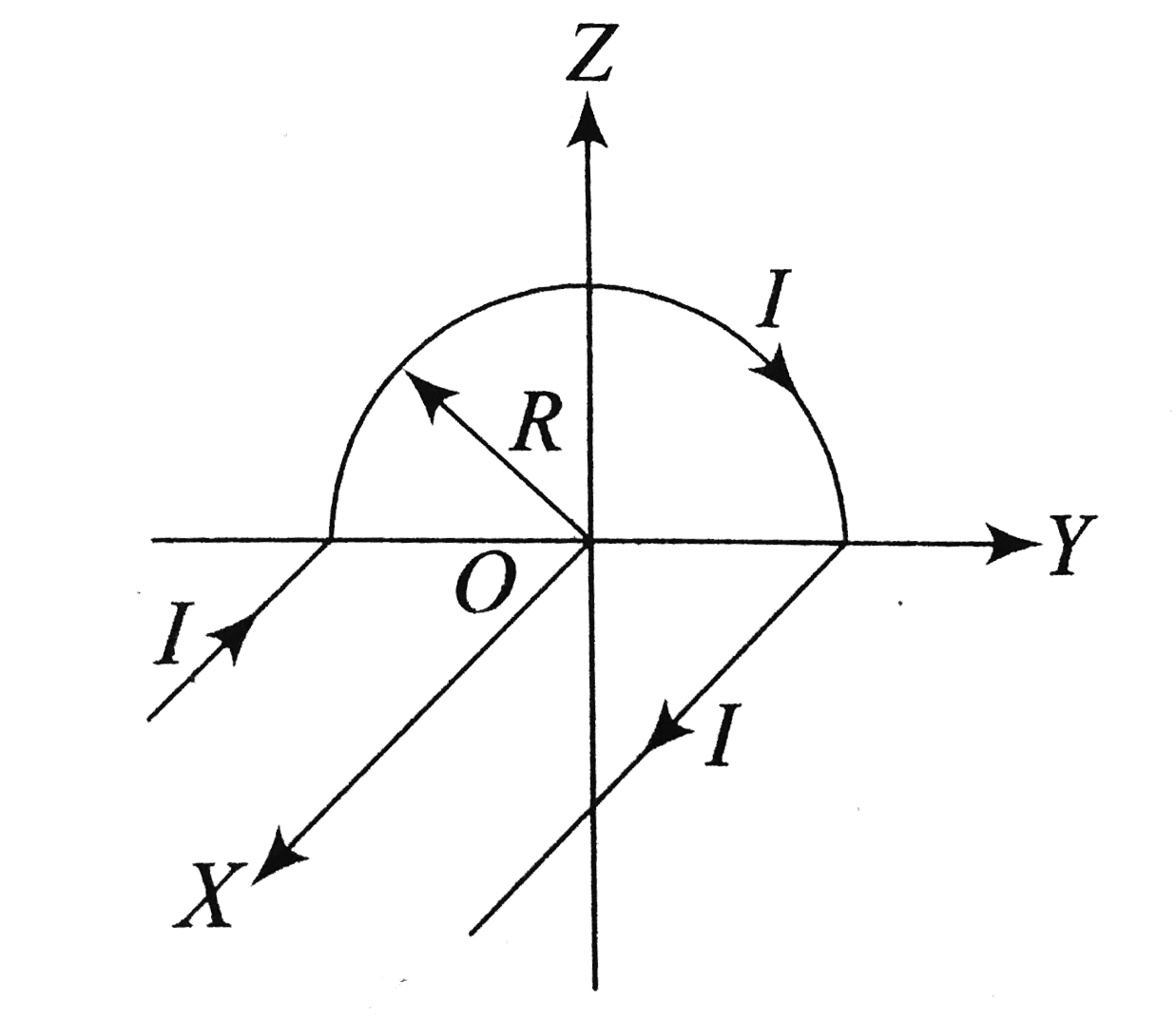
A wire carrying a current I has the shape as show in the adjoining figure. Linear parts of the wire are very long and paralll to x-axis while semicircular portion of radius R lying on the yz-plane. Magnetic field at point O is

→B=μ04πIR(πˆi+2ˆk)
→B=−μ04πIR(πˆi−2ˆk)
→B=−μ04πIR(πˆi+2ˆk)
→B=μ04πIR(πˆi−2ˆk)
The magnetic fields of the linear part of the wire are directed donwards i.e., along the negative z-direction, the value of the magnetic field in each case.
μ04IR
Again, the magnetic field for the semicircular portion of the wire at the point O is directed along the negative x-axis, and its value
=12μ0IR=μ0I4R
∴ Resultant magnetic field
=−ˆkμ04πIR−ˆkμ04πIR−ˆiμ0I4R
=μ04πIR(πˆi+2ˆk)
The opiton (C) is correct.
Topper's Solved these Questions
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NEET
6 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - CBSE SCANNER
26 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - JEE MAIN
7 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
- ELEMENTARY PHENOMENA OF ELECTROSTATICS BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE
2 Videos
Similar Questions
A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View Solution
Knowledge Check
A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
 A→B=μ04πIR(πˆi+2ˆk)B→B=−μ04πIR(πˆi−2ˆK)C→B=−μ04πIR(πˆi+2ˆk)D→B=μ04πIR(πˆi−2ˆK)
A→B=μ04πIR(πˆi+2ˆk)B→B=−μ04πIR(πˆi−2ˆK)C→B=−μ04πIR(πˆi+2ˆk)D→B=μ04πIR(πˆi−2ˆK)A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
 A→B=−μ04πIR(μˆi×2ˆk)B→B=−μ04πIR(μˆi+2ˆk)C→B=−μ04πIR(πˆi−2ˆk)D→B=−μ04πIR(πˆi+2ˆk)
A→B=−μ04πIR(μˆi×2ˆk)B→B=−μ04πIR(μˆi+2ˆk)C→B=−μ04πIR(πˆi−2ˆk)D→B=−μ04πIR(πˆi+2ˆk)A wire carrying current I has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicircular portion of radius R is lying in Y-Z plane. Magnetic field at point O is
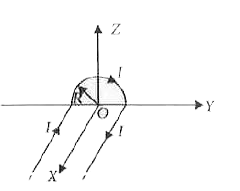 A→B=−μ04πIR(πˆi+2ˆk)B→B=μ04π.IR(πˆi−2ˆk)C→B=μ04π.IR(πˆi−2ˆk)D→B=−μ04π.IR(πˆi−2ˆk)
A→B=−μ04πIR(πˆi+2ˆk)B→B=μ04π.IR(πˆi−2ˆk)C→B=μ04π.IR(πˆi−2ˆk)D→B=−μ04π.IR(πˆi−2ˆk)
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)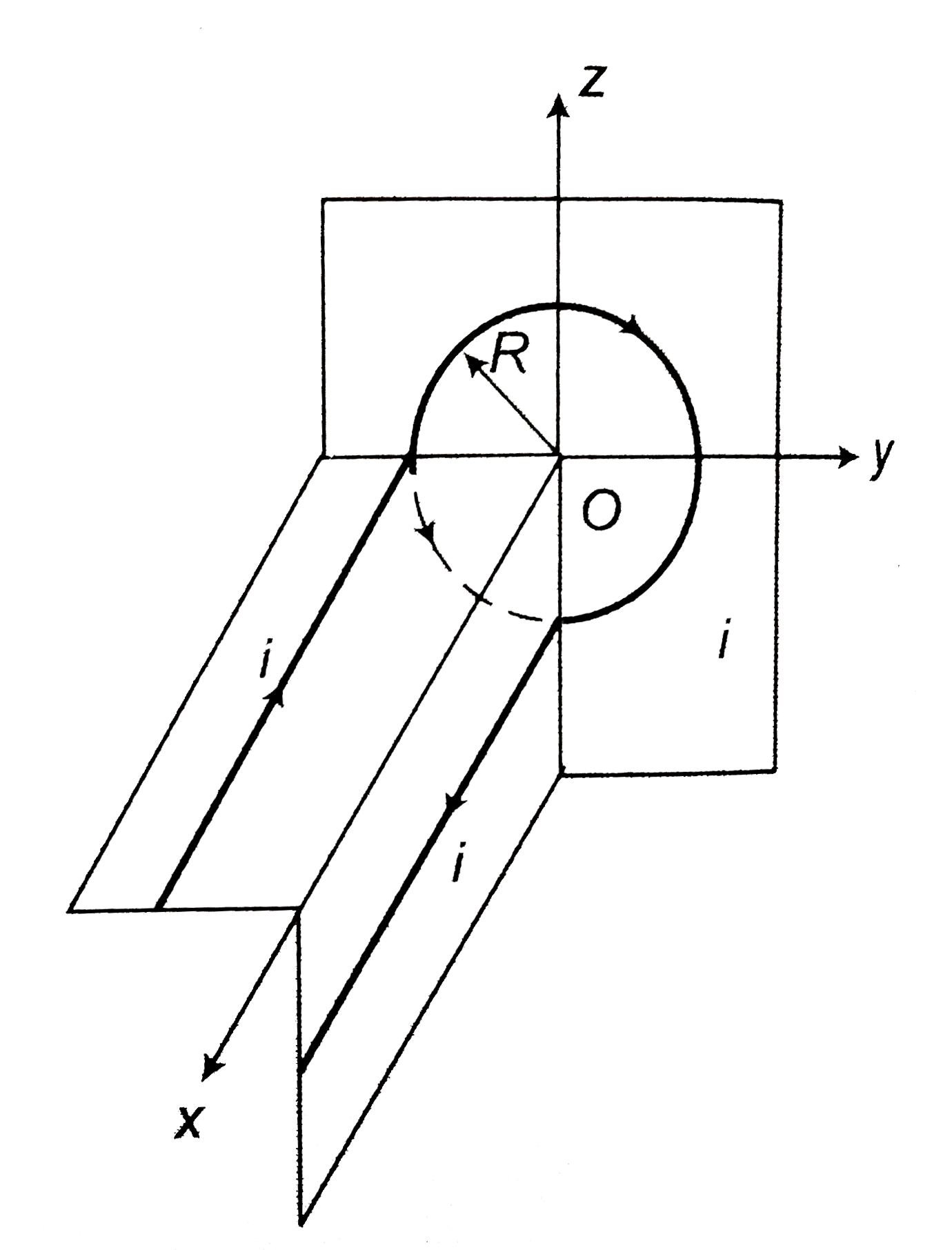
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
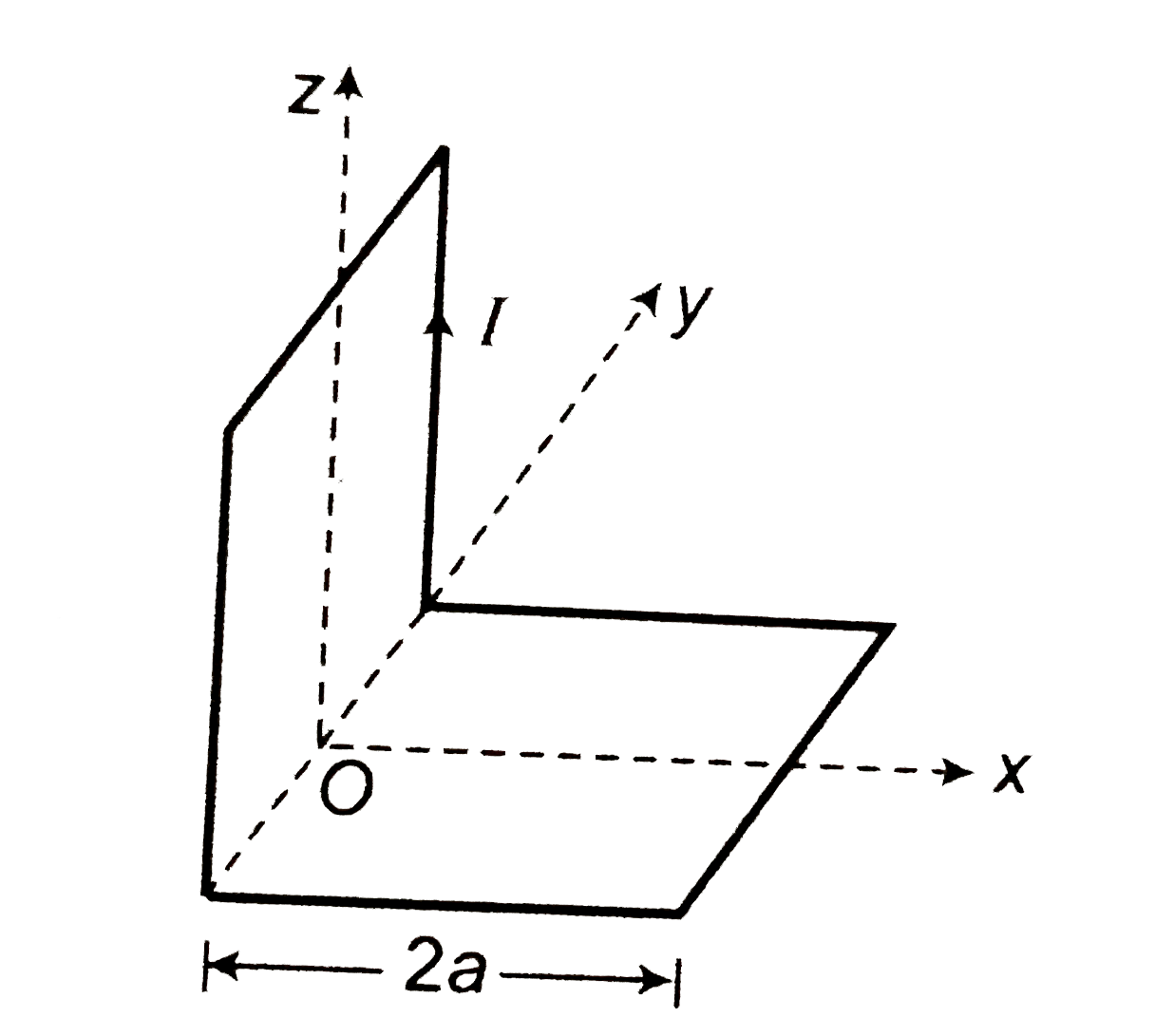
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View Solution
