If Bohr 's quantisation postulate (angular momentum =nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantisation of planets around the sun?
In case of planetary motion, the value of angular momentum is much larger than the value of h ( in case of earth its value is 1070h). As a result the value of n becomes nearly 1070 , making the difference between the successive energy levels infinitesimally small and the levels may be considered continuous.
Topper's Solved these Questions
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT (Multiple Options Correct)
10 Videos
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - EXERCISE(Multiple Choice Questions)
28 Videos
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - Higher Order Thinking Skill (Hots ) Questions
22 Videos
- ALTERNATING CURRENT BOOK - CHHAYA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CBSE SCANNER
33 Videos
- ATOMIC NUCLEUSBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMIC NUCLEUSEXERCISE - CBSE SCANNER
14 Videos
Similar Questions
If Bohr’s quantization postulate (angular momentum = nh/2π ) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantization of orbits of planets around the sun?
View SolutionIf Bohr's qunatisation postulate (angular momentum=nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do never speak of quantization of orbits of planets around the sun?
View Solution
Knowledge Check
The key feature of Bohr'[s spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton we will extend this to a general rotational motion to find quntized rotantized rotational energy of a diatomic molecule assuming it to be right . The rate to energy applied is Bohr's quantization condition
it is found that the excitation from ground to the first excited state of rotation for the CO molecule is close to 4π×1011Hz then the moment of inertia of CO molecule about its center of mass is close to
(Takeh=2π×10−34Js)A2.76×10−46kgm2B1.87×10−46kgm2C4.67×10−47kgm2D1.17×10−47kgm2The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
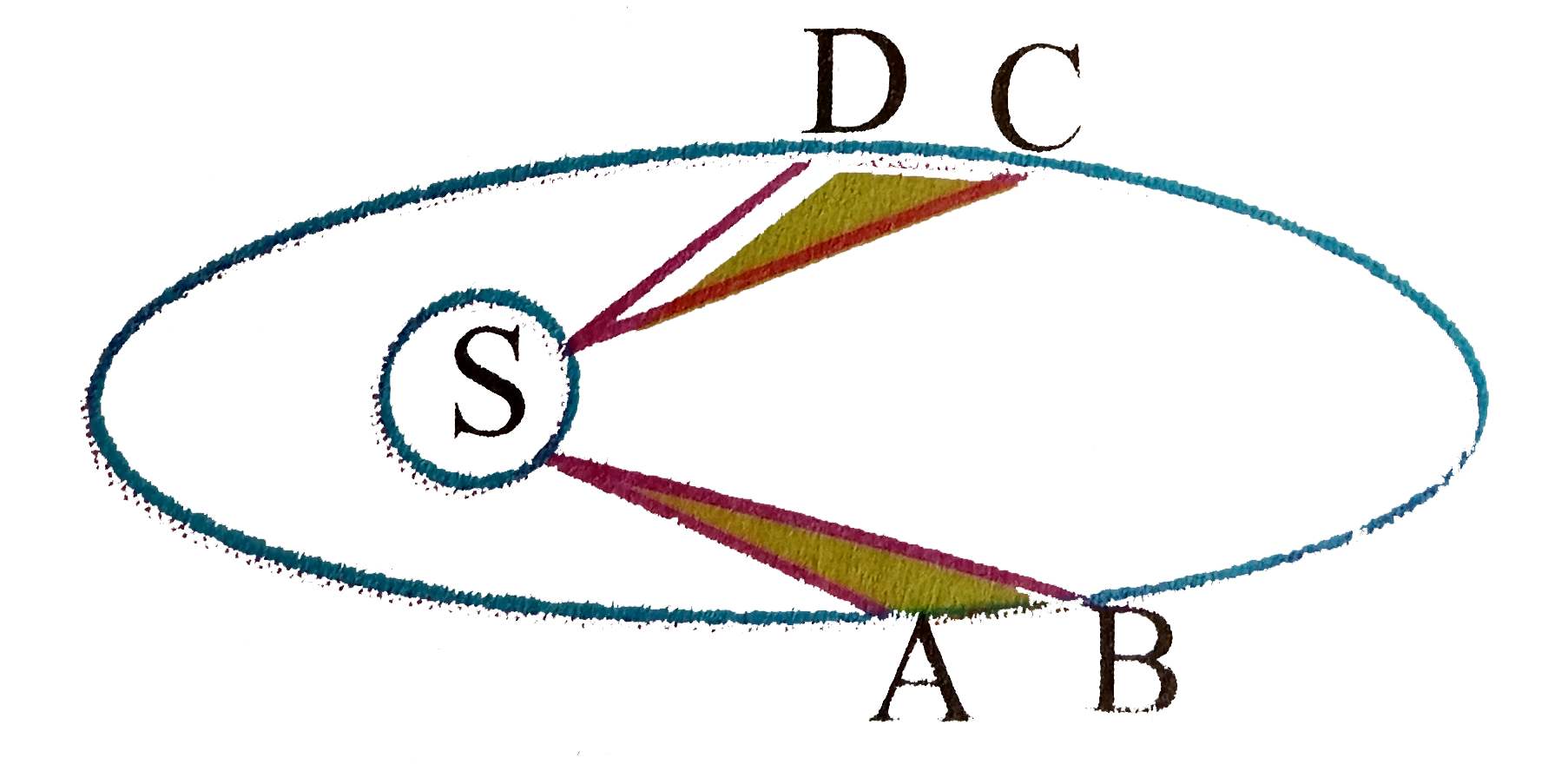 A3GMmaB5GMmaCGMmaDnone of the above
A3GMmaB5GMmaCGMmaDnone of the aboveThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
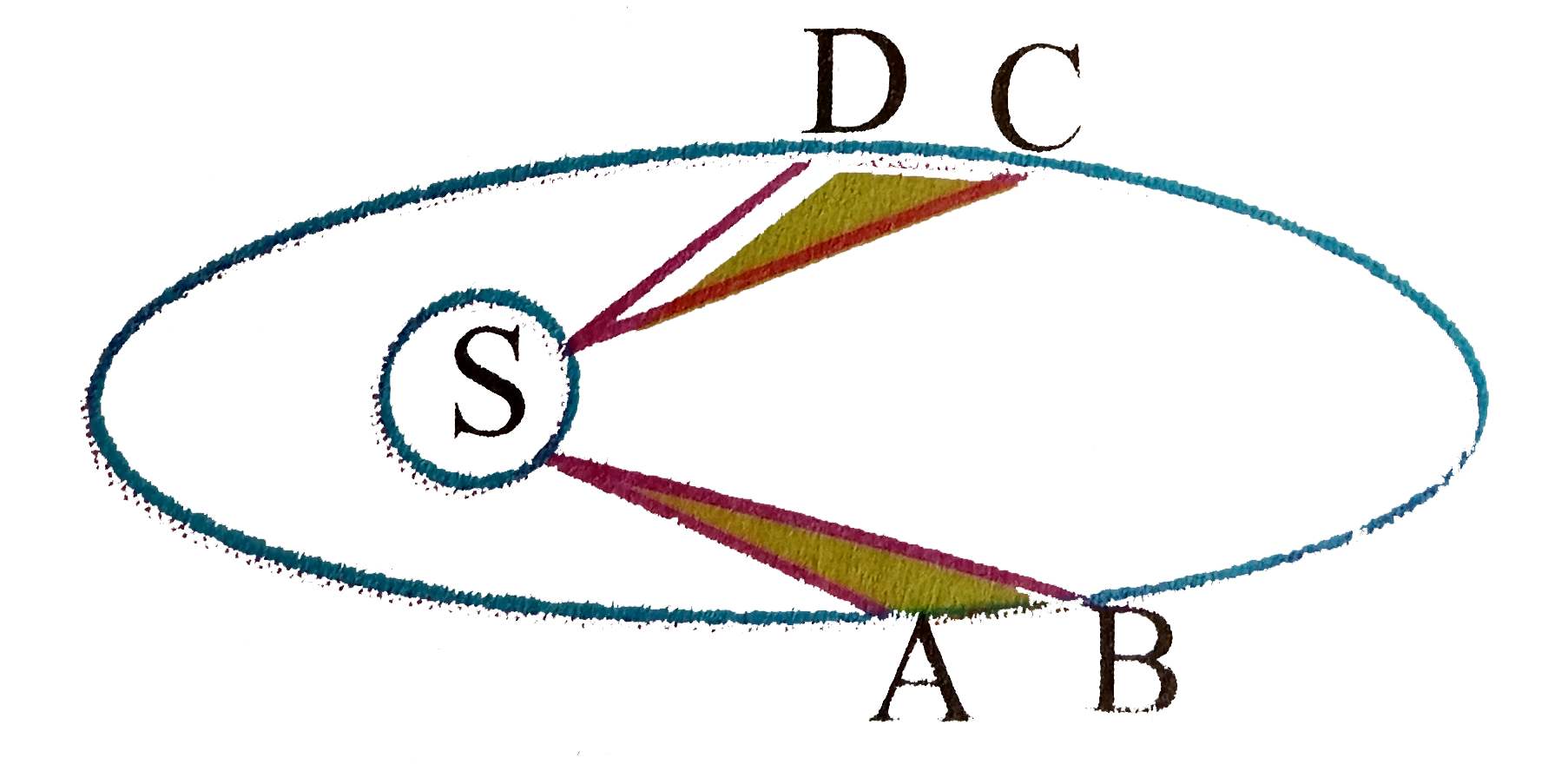 A−3GMm4aB−3GMm8aC−GMm5aDnone of these
A−3GMm4aB−3GMm8aC−GMm5aDnone of these
If Bohar 's quantisation postulate ( angular momentum = nh/2π) is a basic law of nature , it should be equal be equally valid for the case of planetary motion also . Why then do we never speak of quatisation of orbit of planets around the Sun ?
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
it is found that the excitation from ground to the first excited state of rotation for the CO molecule is close to 4π×1011Hz then the moment of inertia of CO molecule about its center of mass is close to
(Takeh=2π×10−34Js)
View SolutionWhile studying the theory of planetary motion, kepler established three laws. According to kepler's second law, the line joining a planet to the sun sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant. This led him to conlude from the sun.
Read the above passege and answer the following questions :
(i) What is the basis of kepler's second law?
(ii) Mercury is closer to the sun than the earth. Will time period of mercury be less or more than one year ? Why ?
(iii) What value of life do you learn from kepler's second law?
View SolutionConsider a system containing a negatively charge poin (π,mπ=273∘me) orbital around a staionary nucleus of atomic number Z .The total energy (En) of ion is half of its potential energy (PEn) in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The longest wavelength radiation emitted in the emission spectrum when the pion de-excited from n=3 to ground state lies which of the following region ?
View SolutionConsider a system containing a negatively charge poin (π,mπ=273∘me) orbital around a staionary nucleus of atomic number Z .The total energy (En) of ion is half of its potential energy (PEn) in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The longest wavelength radiation emitted in the emission spectrum when the pion de-excited from n=3 to ground state lies which of the following region ?
View Solution
