A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
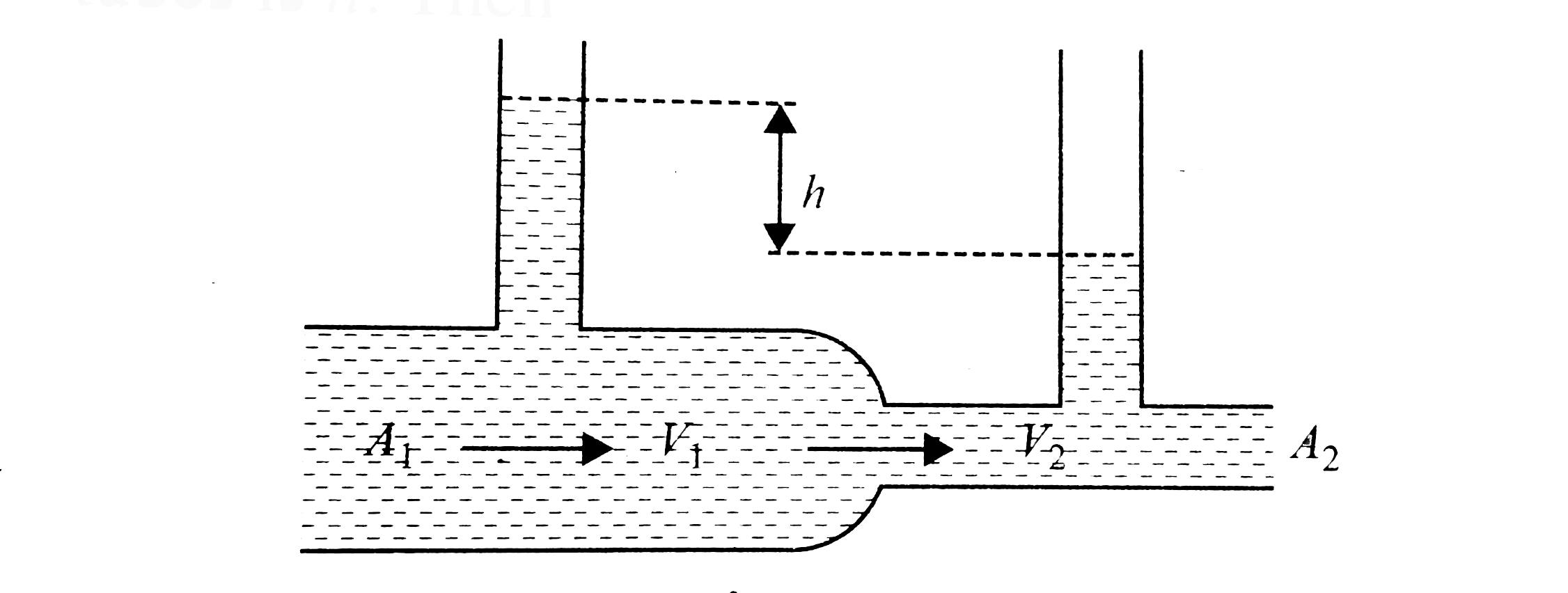
The volume of the liquid flowing through the tube in unit time is A1v1
v2−v1=√2gh
v22−v21=2gh
The energy per unit mass of the liquid is the same in both sections of the tube
The correct Answer is:A, C, D
Step by step video, text & image solution for A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A_(1) and A_(2) are v_(1) and v_(2) respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - FLUID MECHANICSEXERCISE - Critical Thinking14videos
FLUID MECHANICS
- BOOK - ERRORLESS CHAPTER - FLUID MECHANICSEXERCISE - Graphical Questions5videos
FLUID MECHANICS
- BOOK - ERRORLESS CHAPTER - FLUID MECHANICSEXERCISE - Pascal s Law and Archmidies Principle27videos
FLUID MECHANICS
- BOOK - ERRORLESS CHAPTER - ELASTICITYEXERCISE - Self Evaluation Test11videos
ELASTICITY
- BOOK - ERRORLESS CHAPTER - FRICTIONEXERCISE - MCQ S125videos
FRICTION
Similar Questions
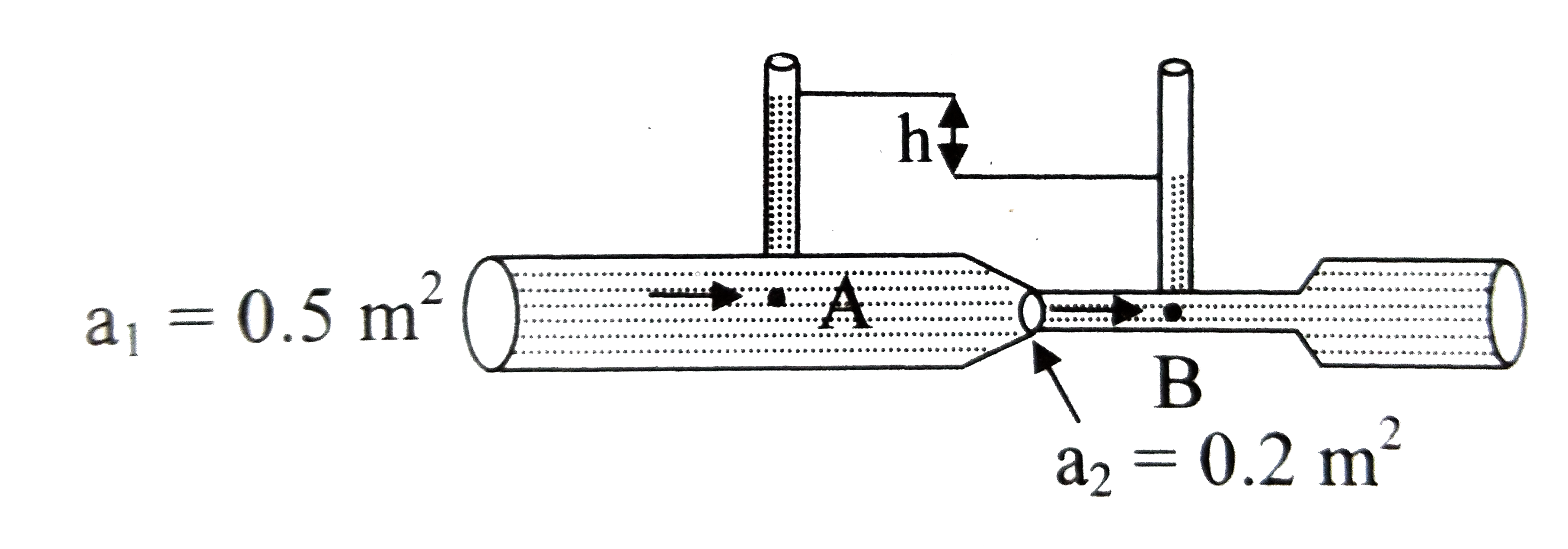
An incompressible, non-viscous liquis of density r flows through a horizontal tube as shown below. The flow condition is steady. Area of cross section at A and B are a1anda2 respectively. The height difference of liquid in two tubes inserted at A and B is h.
 View Solution
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are 4cm2and2cm2 respectively, find the rate of flow of water across any section.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh - Question 2 - Select One
From a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.
 AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube - Question 3 - Select One
An incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:
 A3.0 m/sB1.5 m/sC1.0 m/sD2.25 m/s
A3.0 m/sB1.5 m/sC1.0 m/sD2.25 m/s
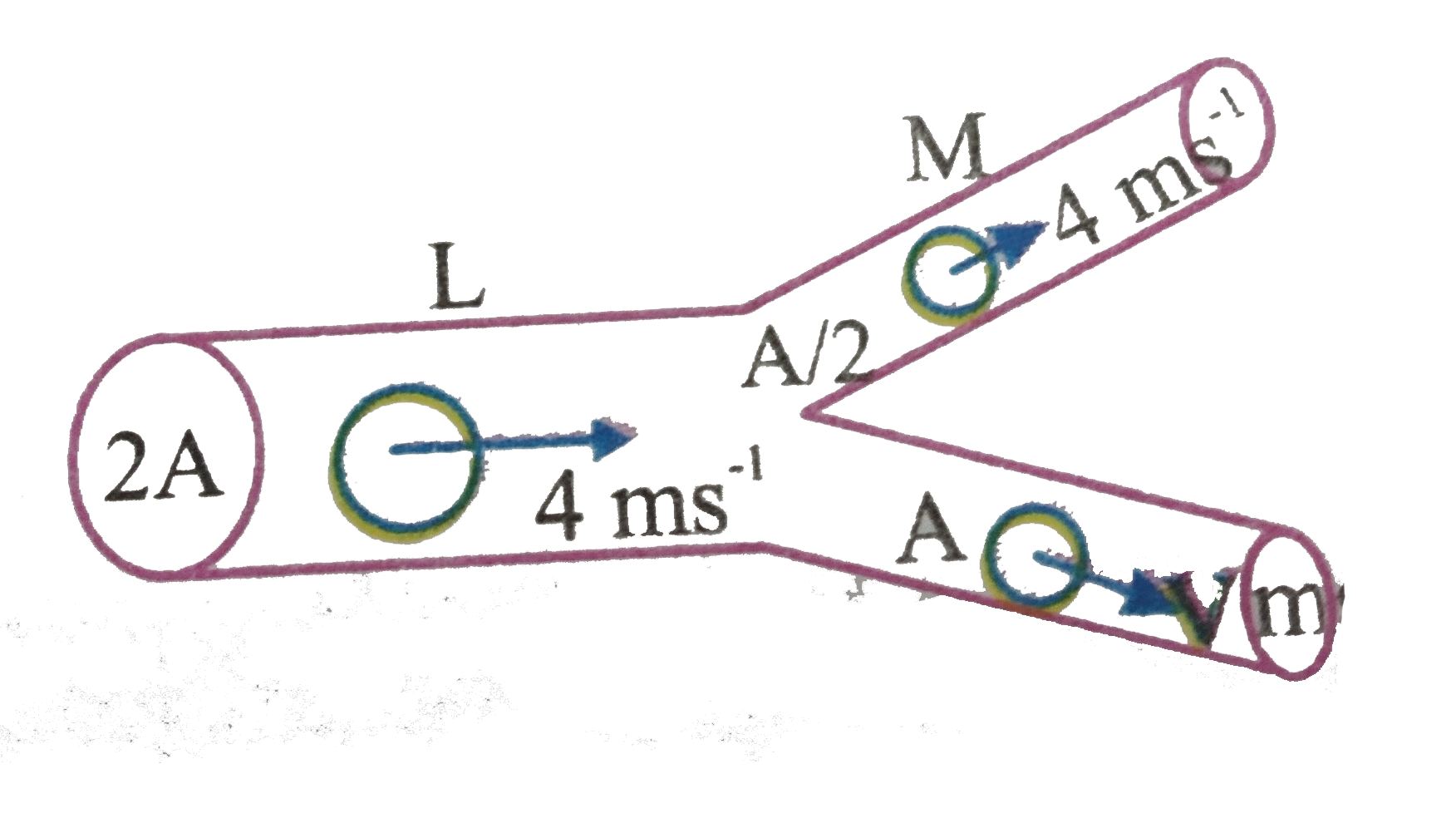
An incompressible liquid flows through a horizontal tube LMN as shown in the figure. Then the velocity V of the liquid throught he tube N is:View SolutionThe mass of the liquid flowing per second per unit area of cross section of the tube is proportional to Pxandvy , where P is the pressure difference and v is the velocity , then the relation between x and Y is
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :View SolutionA liquid flows through a pipe of non-uniform cross-section. If A1andA2 are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
View SolutionFig, shows a U-tube of uniform cross-sectional area A accelerated with acceleration a as shown. If d is the seperation between the limbs. Then the difference in the levels of the liquid in the U−tube is
 View Solution
View Solution

