Select the correct statement with reference to van der Waal's ga.

The compressibility factor for gas at critical state is $\frac{8}{3}$

At critical temperature, real gas behave like an ideal gas

At Boyle's temperature, real gas behaves like an ideal gas at all pressure

At Boyle's temperature, gas cannot be liquefied

Video Solution

Text Solution

Verified by Experts

The correct Answer is:d

Answer

Step by step video, text & image solution for Select the correct statement with reference to van der Waal's ga. by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 CHEMISTRY STATES OF MATTER

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
In the van der Waals equation
A $b$ is the volume occupied by the gas molecules
B $b$ is four times the volume occupied by the gas molecules
C $b$ is the correction factor for intermolecular attraction
DNone of these
Question 2 - Select One
Select the incorrect option for van der Waal's gas.
AHe has smaller 'a' (van der Waals' constant) than Ne,Kr,Ar, $C O_{2}, C H_{4}$ and $N H_{3}$
BHe hs smaller 'b' (van der Waals' constant)than Ne,Kr,Ar, $C O_{2}, C H_{4}$ and $N H_{3}$
CAt 273K and 1 atm, He moecules have attractions with respect to ideal behaviour
DAt 273 K and 1 atm He molecules have repulsions with respect to ideal behaviour
Question 3 - Select One or More
Figure displays the plot of the compression factor Z versus P for a few gases which of the following statements is/are correct for a van der Waals' gas?

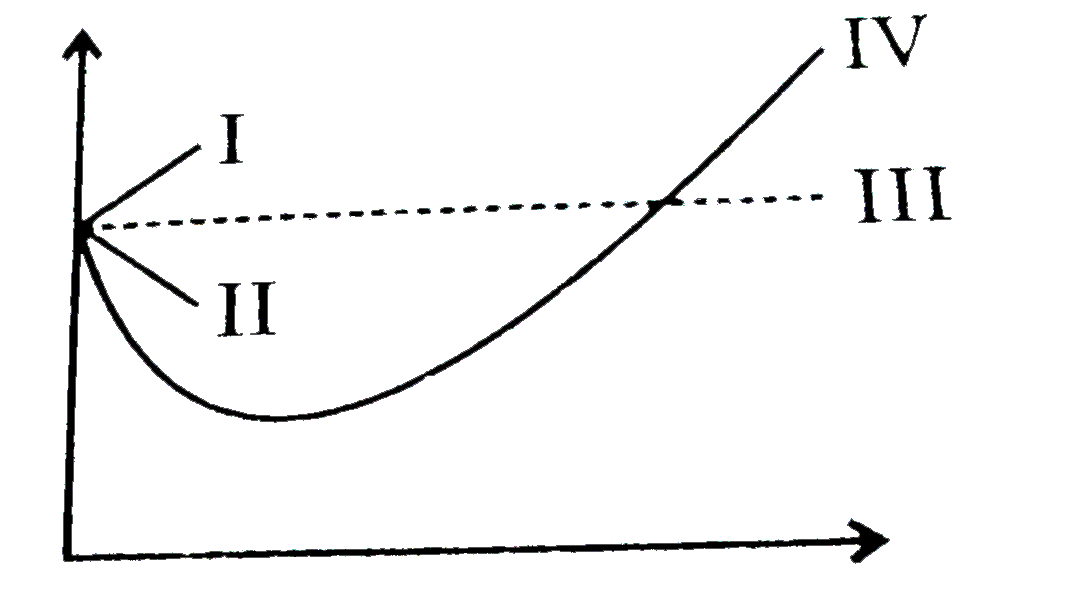AThe plot I is applicable provided the van der Waals' constant a is negligible
BThe plot II is applicable provided the van der waals' constant b is negligible
CThe plot III is applicable provided the van der waals' constant a and b are negligible
Dthe plot IV is applicable provided the temperature of theh gas is must higher than its critical temperature.