Under a given condition, it is found that two separate gases effuse out of two separate containers in such a way that they follow the equation dNdt=−K1NanddNdt=−K2NK1=6.93×10−2sec−1.K2=6.93×10−5sec where N is no of molecule remaining in the container.
Which one of the following may represent fraction of number of molecules present after the given interval for gas-I?
t=0t=100sect=200sec
1 1218
t=0t=100sect=200sec
118116
t=0t=100sect=200sec
1 1214
t=0t=100sect=200sec
114116
The correct Answer is:c
Step by step video, text & image solution for Under a given condition, it is found that two separate gases effuse out of two separate containers in such a way that they follow the equation (dN)/(dt)=-K_(1)N and (dN)/(dt)=-K_(2)N K_(1)=6.93xx10^(-2) sec^(-1). K_(2)=6.93xx10^(-5) sec where N is no of molecule remaining in the container. Which one of the following may represent fraction of number of molecules present after the given interval for gas-I? by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If a closed container contain 5 moles of CO2 gas, then find total number of CO2 molecules in the container (NA=6×1023)
View SolutionThe substance undergoes first order decomposition. The decomposition follows two parallel first order reactions as :
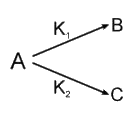
K1=1.26×10−4sec−1andK2=3.8×10−5sec−1 The percentage distribution of B and C
View Solution
Knowledge Check
Under a given condition, it is found that two separate gases effuse out of two separate containers in such a way that they follow the equation dNdt=−K1NanddNdt=−K2NK1=6.93×10−2sec−1.K2=6.93×10−5sec where N is no of molecule remaining in the container.
Identify the correct option regarding sequence of (True) and (False) statements
(i) The time required for moles of gas I to get reduced to half of original and that of gas II to be reduced to half of original is independent of initial moles of gas I and gas II.
(ii) THe rate at which initially molecules will come out in gas I as comapred to gas II will be greater in gas II if initial number of molecules are same.
(iii) The time required for moles to get reduced from 1 to 0.8 in gas I and 2 to 1.6 in gas II will be same.
(iv) for the two gases, moles remaining in the container after some ubterval should be in Geometrical Progression.ATFFTBTFTTCFTFTDTTFFFor 2Ak1−−→Bk2−−→3C.K1=2×10−4sec−1andk2=3×10−4/mol-sec. {d[B]/dt} equal to :
Ak1[A]−k2[B]Bk1[A]2−k2[B]Ck1[A]−k2[B]2Dk1[A]2−k2[C]3A substance undergoes first order decomposition. The decomposition follows two parallel first order reaction as:
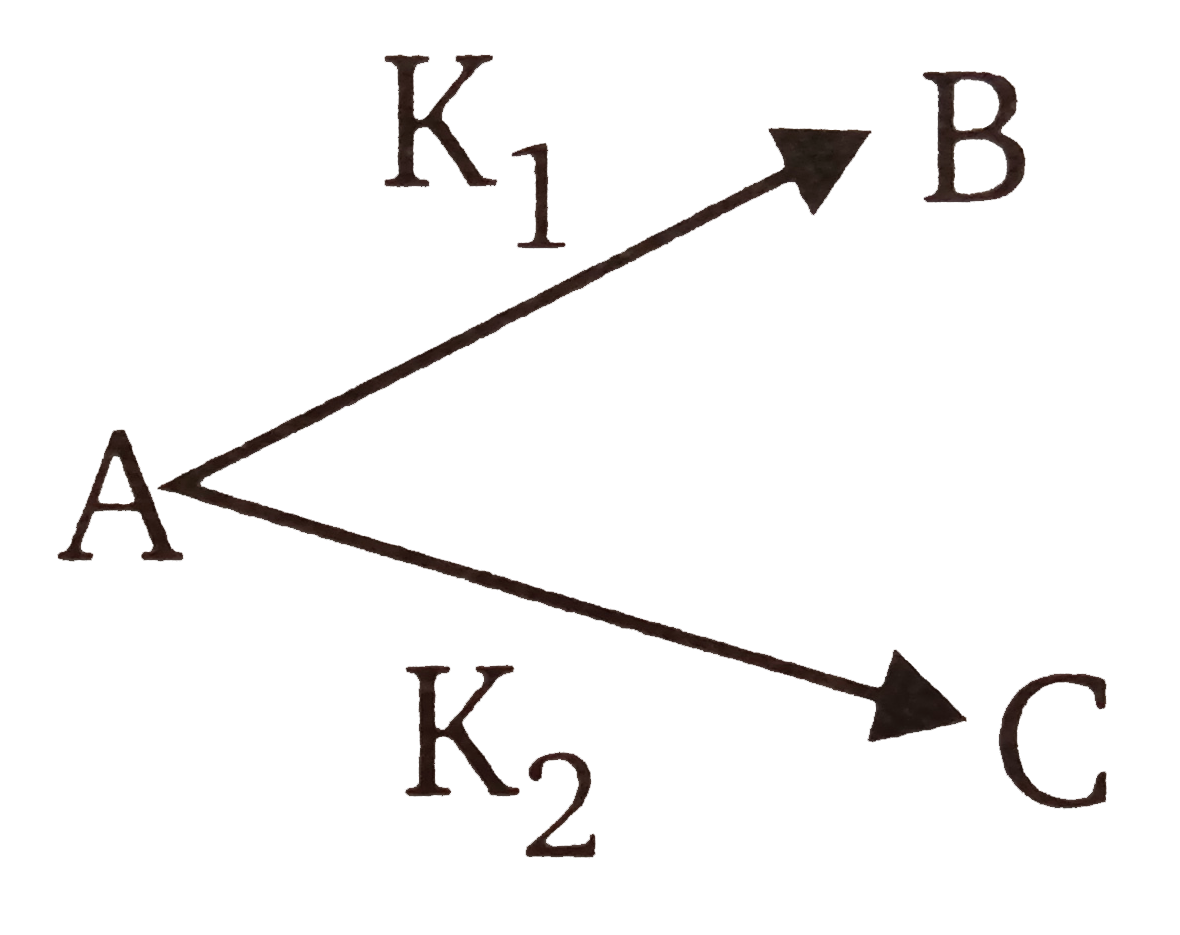and KP1=1.26×10−4sec−1
K2=3.80×10−5sec−1
The percentage distribution of B and C are:A80%Band20%CB76.83%Band231.7%CC90%Band10%CD60%Band40%C
A substance undergoes first order decomposition. The decomposition follows two parallel first order reactions as
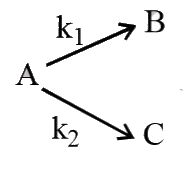, k1=1.26×10−4 sec−1andk2=3.6×10−5 sec−1 Calculate the % distribution of B & C.
View SolutionA certain gas A polymerizes to a small extent at a given temperature and pressure, nA⇔An. Show that the gas obeys the approx. equation PVRT=[1−(n−1)KcVn−1], where Kc=[An][A]n and V is the volume of the container. Assume that initially one mole of A was taken in the container.
View SolutionA compound A dissociate by two parallel first order paths at certain temperature
A(g)k1(min−1)→2B(g)k1=6.93×10−3min−1
A(g)k2(min−1)→C(g)k2=6.93×10−3min−1
If reaction started with pure 'A' with 1 mole of A in 1 litre closed container with initial pressure (in atm) developed in container after 50 minutes from start of experiment?
View SolutionA compound A dissociates by two parallel first order paths at certain temperature
A(g)k1(−1min)−−−−−−→2B(g) k1=6.93×10−3−1min
A(g)k1(−1min)−−−−−−→C(g) k2=6.93×10−3−1min
The reaction is started with 1 mole of pure 'A' litre closed container with initial pressure 2 atm. What is the pressure (in atm) developed in container after 50 minutes from start of experiment?
View SolutionA gas at 300 K has pressure 4×10−10N/m2. IF k=1.38×10−23J/K, the number of molecule/cm3 is of the order of
View Solution