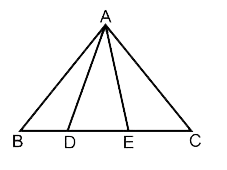
In the given figure, AD = AE and $A D^{2} = B D \times E C$ prove that: triangles ABD and CAE are similar.

Video Solution

Text Solution

Verified by Experts

AD=AE
$∠ A D E = ∠ A E D$
$∠ A D B = ∠ A E C$
$A D^{2} = B D \cdot E C$
$\frac{A D}{B D} = \frac{E C}{A D}$
$\frac{A D}{B D} = \frac{E C}{A E}$
$I n ∠ A B D and ∠ C A E$
$\frac{A D}{B D} = \frac{E C}{A E}$
$∠ A D B = ∠ A E C$ $∠ A B D ≅ ∠ C A E$ .

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

In the given figure, AB = AC and AD = AE. Prove that:
BD = CE

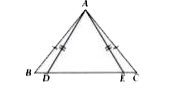
View Solution
In the given figure, AB = AC and AD = AE. Prove that:
$Δ A B D ≅ Δ A C E$

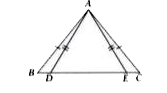
View Solution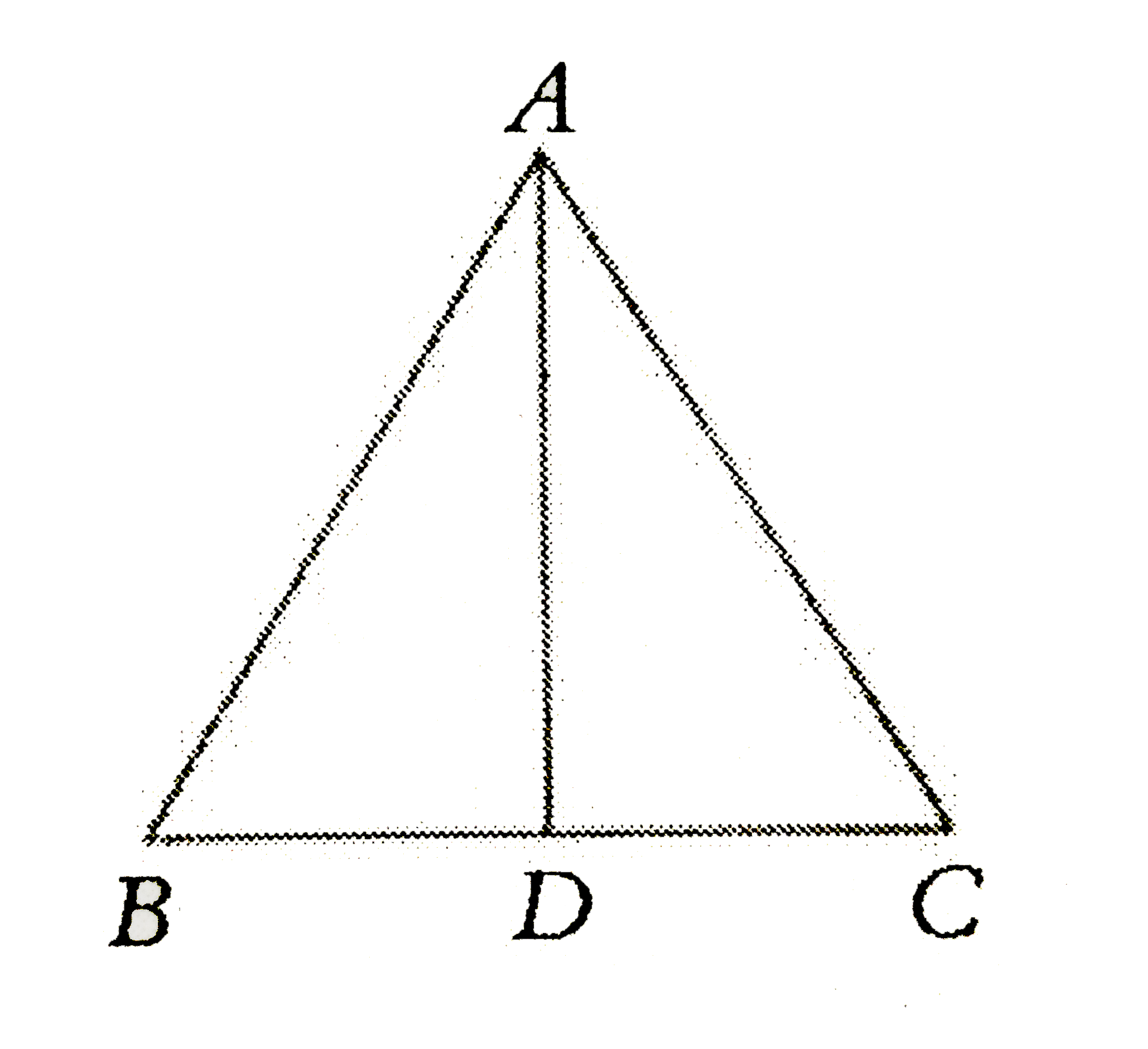
In the given figure, AD is the bisector of $∠ B A C$ . Prove that triangles ABD and ADC are congruent, if AB=AC.
View Solution
In the given figure, $A B ∣ ∣ E C, A B = A C$ and AE bisects $∠ D A C$ . Prove that:
View Solution
In the given figure , if AB = BC , $∠ B A D = ∠ C A E$ then prove that $△ A D E$ is an isosceles triangle .

View Solution
In the given figure of AD = CB then prove that AC = BD
View Solution
In a $A B C, A D ⊥ B C$ and $A D^{2} = B D \times C D .$ prove that $A B C$ is a right triangle.
View Solution
In the given figure, $\frac{A D}{D B} = \frac{A E}{E C}$ and $∠ A D E = ∠ A C B$ . Prove that $Δ A B C$ is an isosceles triangle.

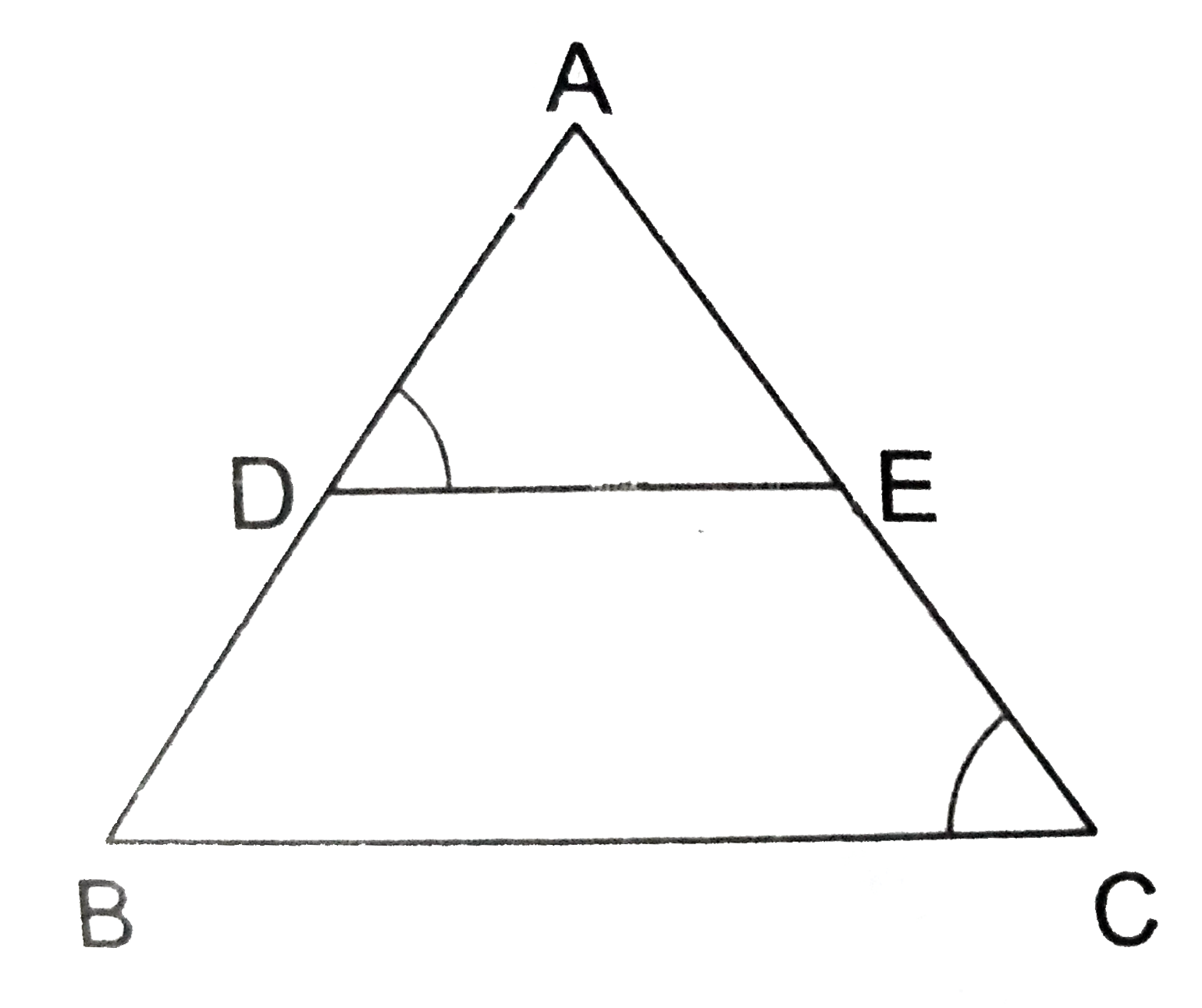
View Solution
In the given figure, DE // BC.

Prove that $Δ A D E and Δ A B C$ are similar
View Solution
In a $A B C, A D ⊥ B C$ and $A D^{2} = B D \times C D .$ Prove that $A B C$ is a right triangle.
View Solution

Recommended Questions

Home
Ask Doubt
Profile