
Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities K1,K2 and K3. The points P and Q are maintained at different temeperature for the heat to flow at the same rate along PRQ and PQ. Whi of the following options correct?
K3=12(K1+K2)
K3=K1+K2
K3=K1K2K1+K2
K3=2(K1+K2)
The correct Answer is:C
Step by step video, text & image solution for Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities K_1,K_2 and K_3. The points P and Q are maintained at different temeperature for the heat to flow at the same rate along PRQ and PQ. Whi of the following options correct? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Graphical Questions17videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Assertion & Reason24videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Radiation (Newton s Law of Cooling)37videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test15videos
THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY
- BOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions333videos
UNITS, DIMENSION & MEASUREMENTS
Similar Questions
Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities k1,k2,k3andk5. When points A and C are maintained at different temperature, no heat flows through the central rod if
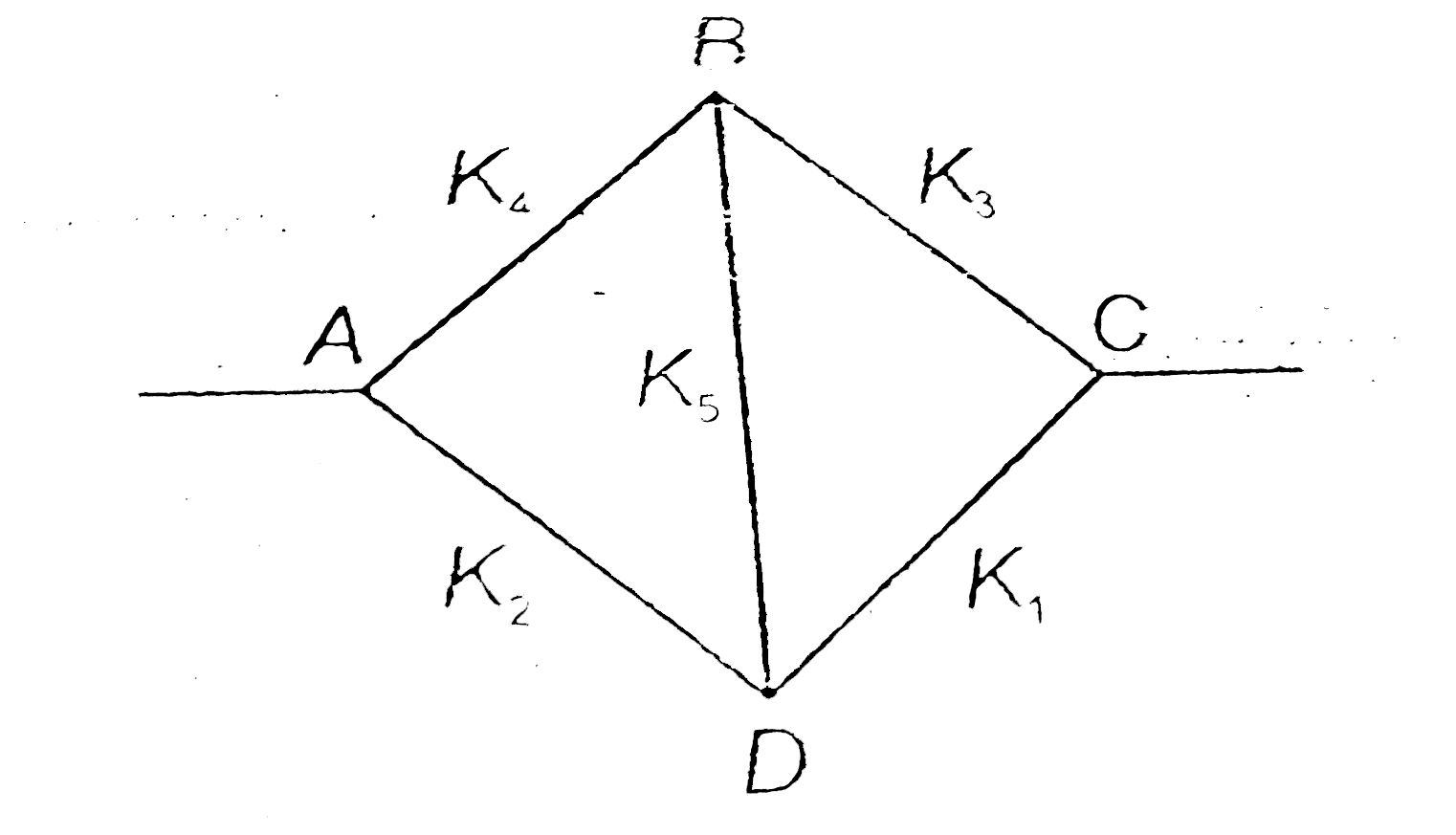 View Solution
View SolutionThree rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state isView Solution
Knowledge Check
- Question 1 - Select One
Five rods of same dimensions are arrranged as shown in the figure. They have thermal conductivities K1,K2,K3,K4 and K5. When points A and B are maintained at different themperature, no heat flows through the central rod if
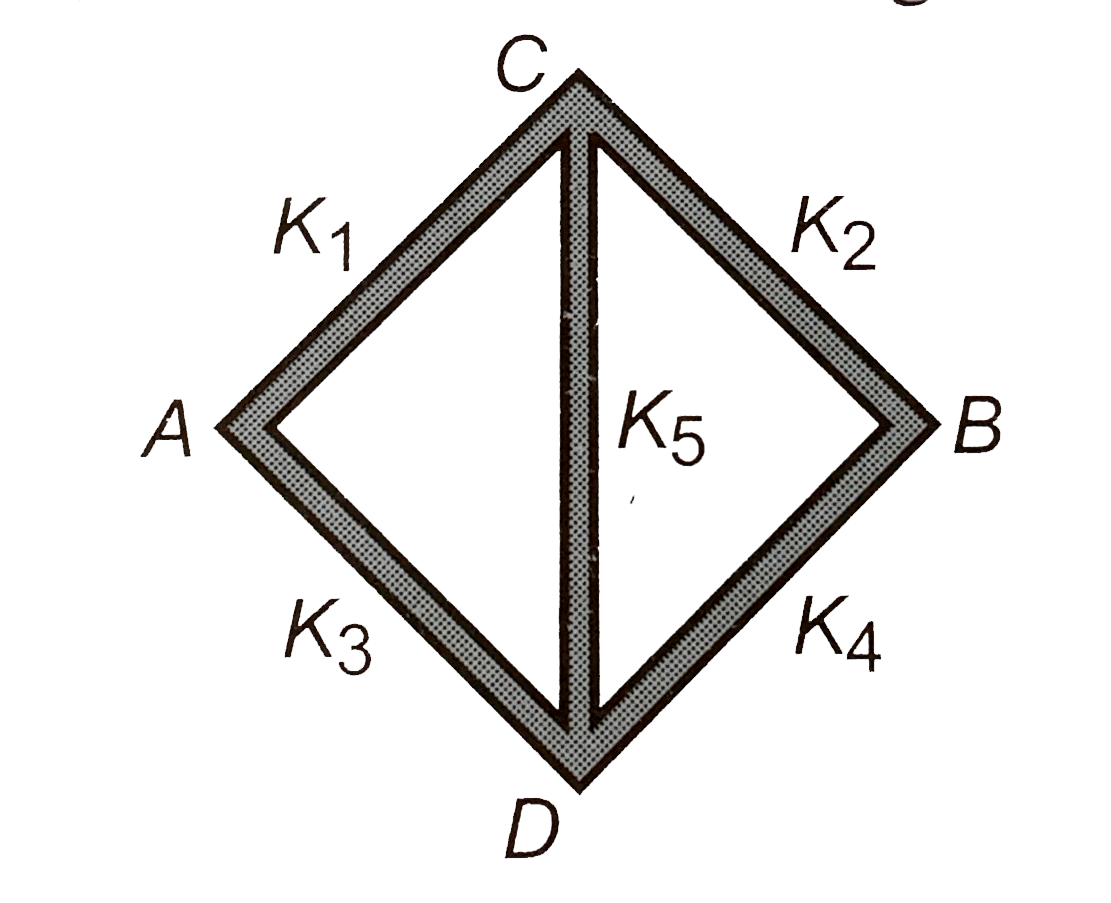 AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3
AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3 - Question 2 - Select One
Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities K1,K2,K3,K4 and K5 . When points A and B are maintained at different temperatures, no heat flows through the central rod if
 AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3
AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3 - Question 3 - Select One
Three rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
Ak1k2k3/k2k3+k1k2+k1k3B3(k1k2k3)/k2k3+k1k2+k1k3Ck1+k2+k3D(k1+k2+k3)/ 3
Three rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
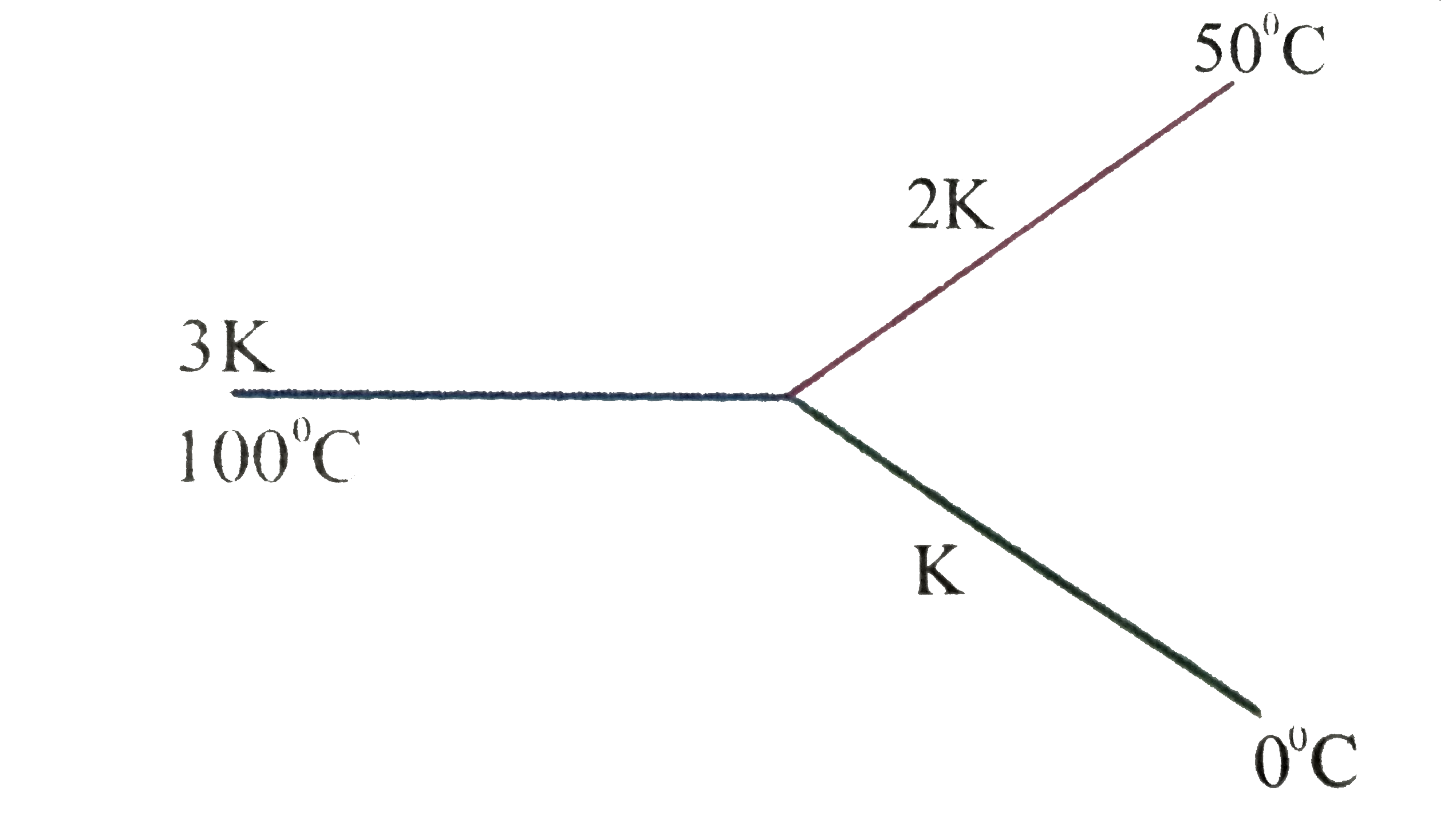 .View Solution
.View SolutionThree rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .View Solution
.View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
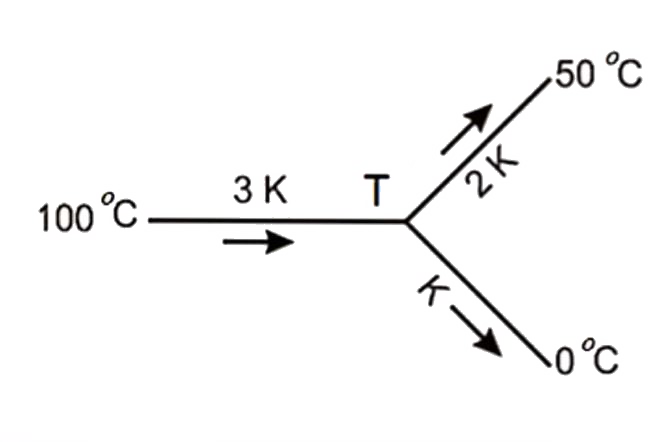 View Solution
View SolutionThree rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png) View Solution
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be
 View Solution
View Solution

