Assertion : An important feature of fluorite structure is that cations being large ib size occupy lattice points, the formula unit (A cation, B anion)
Reason: There are cations and anions per unit cell of the flucrite structure
Statement -1 is True, Statement -2 is true : Statement -2 is a correct explanation for Statement -1
Statement -1 is True, Statement -2 is True , Statement -2 is NOT a correct explanation for Statement -1
Trapped eletrons
Statement -1 and Statement -2 both are False
Step by step video & image solution for Assertion : An important feature of fluorite structure is that cations being large ib size occupy FC C lattice points, the formula unit AB_(2) (A cation, B anion) Reason: There are 6 cations and 12 anions per FC C unit cell of the flucrite structure by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider an ionic solid MX with NaCl structure. Construct a new structure (Z) whose unit cell is constructed from the unit cell of MX following the sequential instructions given below. Neglect the charge balance. 1.Remove all the anions (X) except the central one 2.Replace all the face centered cations (M) by anions (X) 3.Remove all the corner cations (M) 4.Replace the central anion (X) with cation (M)
The value of (number of anion s number of cation s) in z is ________.
View SolutionConsider an ionic solid MX with NaCl structure. Construct a new structure (Z) whose unit cell is constructed from the unit cell of MX following the sequential instructure given below. Neglect the charge balance.
(i) Remove all the anions (X) except the central one
(ii) Replace all the face-centred cations (M) by anions (X)
(iii) Remove all the corner cations (M)
(iv) Replace the central anion (X) with cation (M)
The value of (number of anionsnumber of cations) in Z is .............

View Solution
Knowledge Check
Assertion:- Antigluorite structure is 4:8 (cation:anion) type coordination crystal.
Reason:- Ratio of no. of cation and anions in CaF2 crystal is 1:2AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are False.Give the correct order of initials T (true) or F (False) for following statements.
I. In an anti-fluorite structure anions form FCC lattice and cations occupy all tetrahedral voids.
II. If the radius of cations and anions are 0.2 Å and 0.95 Å then coordinate number of cation in the crystal is 4.
III. An atom/ion is transferred from a lattice site to an interstitial position in Frenkel defect.
IV. Density of crystal always increases due to substitutinal impurity defect.ATFFFBFTTFCTFFTDTFTFAn ionic solid AB crystallizes as a bcc structure . The distance between cation and anion in the lattice is 338 pm . Calculate the edge length of the unit cell .
A195.15 pmB97.58 pmC390.3 pmD780.6 pm
Consider an ionic solid MX with NaCl structure. Construct a new structure (Z) whose unit cell is constructed from the unit cell of MX following the sequential instructions given below. Neglect the charge balance. 1.Remove all the anions (X) except the central one 2.Replace all the face centered cations (M) by anions (X) 3.Remove all the corner cations (M) 4.Replace the central anion (X) with cation (M)
The value of (number of anion s number of cation s) in z is ________.
View SolutionConsider an ionic solid MX with NaCl structure. Construct a new structure (Z) whose unit cell is constructed from the unit cell of MX following the sequential instructions given below. Neglect the charge balance.
(i) Remove all the anions (X) except the central one
(ii) Replace all the face centered cations (M) by anions (X)
(iii) Remove all the corner cations (M)
(iv) Replace the central anion (X) with cation (M)
The value of (number of anionsnumber of catons) in Z is ____
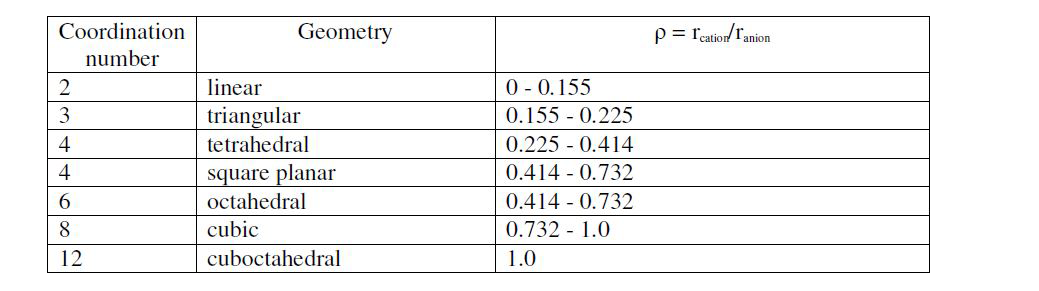
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
A solid AB has square planar structure. If the radius of cation A+ is 120pm,Calculate the maximum possible value of anion B−
View SolutionAn ionic compound is made up of cations A and anions B. if cations A are at the alternate corners and anions are at the alternate faces of the cubic unit cell then empirical formula of the compound will be
View SolutionStructure of ionic compounds
The bigger atom or ion will form the lattice and smaller atom/ion will occupy the voids generally the bigger ion is anion and smaller ion is cation in ionic compounds.The type of void occupied by the cation is decided by radius ratio.

Find the correct set of combination for the compound whose cation has its nearest cationic neighbour at a distance of (a√2) where 'a' is the length of unit cell.
View Solution
