Statement -I : Probability density of electron is zero at nucleus for all p & d orbitals.
Statement -II : Probability density of electron at the nucleus depends upon azimuthal quantum number
only.
If both Statement -I & Statement -II are True & the Statement -II is a correct explanation of the Statement
I.
If both Statement -I & Statement -II are True but the Statement -II is not a correct explanation of the
Statement- I.
If Statement -I is True but the Statement -II is False.
If Statement -I is True but the Statement -II is True .
The correct Answer is:C
Probability density of electron at the nuclues depends upon principle quantum number as well as azimauthal
quamtum number
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - BANSALCHAPTER - ATOMIC STRUCTUREEXERCISE - MULTIPLE CORRECT CHOICE TYPE
19 Videos
- ATOMIC STRUCTUREBOOK - BANSALCHAPTER - ATOMIC STRUCTUREEXERCISE - MATCH THE COLUMN
10 Videos
- ATOMIC STRUCTUREBOOK - BANSALCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise.2
21 Videos
- GENERAL ORGANIC CHEMISTRYBOOK - BANSALCHAPTER - GENERAL ORGANIC CHEMISTRYEXERCISE - Exercise 3
9 Videos
Similar Questions
Knowledge Check
The probability density curve for 2s electron appears like
A B
B C
C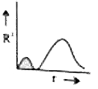 D
D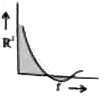
The probability density curve for 2s electron appears like
A B
B C
C D
D
Speed of a revolving electron around the nucleus varies with principal quantum number n as :
Av∝mBv∝n2Cv∝1nDv∝1n2
The correct statement about probability density (except at infinite distance from nucleus ) is :
View SolutionMatch the entires in Column I with the correctly related quantum number(s) in Column II.
ColumnIColumnIIOrbital angular momentum of the electron in a hydrogen-like atomic orbitalp.Principal quantum numberA hydrogen-like one-electron wave function obeying Pauli's principleq.Azimuthal quantum numberShape size and orientation of hydrogen-like atomic orbitalsr.Magnetic quantum numberProbability density of electron at the nucleus in hydrogen-like atomsElectron spin quantum number
View SolutionMatch the entries in Column I with the correctly related quantum number(s) in Column II. Indicate your answer by darkening the appropriate bubbles of the 4×4 matrix given in the ORS.
Column IColumn II(A)Orbital angular momentum of the(P)Principal quantum numberelectron in a hydrogen-like atomic orbital(B)A hydrogen-like one-electron wave(Q)Azimuthal equation numberfunction obeying Pauli principle(C)Shape.size and orientation of hydrogen like atomic orbitals(R)Magnetic quantum number(D)Probability density of electron at the nucleus(S)Electron spin quantum numberin hydrogen-like atom
View SolutionElectron density order in the benzene nucleus is
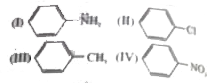
View SolutionWhich orbital give an electron the greatest probability of being found close to the nucleus
View Solution