The diamagnetic complex which has two geometrical and 4 optically active isomers is :
[Co(gly)3]
[Pt(en)2Cl2]2+
[Co(en)3]3+
[Fe(Ox)3]3−
The correct Answer is:A
To solve the question regarding the diamagnetic complex that has two geometrical and four optically active isomers, we will analyze the given complexes step by step.
Step 1: Identify the Complex
We need to identify a complex that is diamagnetic, has two geometrical isomers, and four optically active isomers. The complex mentioned in the video is (Co(Gly)3) where Glycine acts as a bidentate ligand.
Step 2: Understanding Bidentate Ligands
Glycine (Gly) is a bidentate ligand, meaning it can coordinate to the metal center through two different donor atoms. In this case, Glycine coordinates through its nitrogen and oxygen atoms.
Step 3: Determine the Geometry
The complex (Co(Gly)3) has an octahedral geometry because it is a coordination complex with a central metal ion surrounded by six donor atoms (three Glycine ligands).
Step 4: Identify Geometrical Isomers
In an octahedral complex with bidentate ligands, we can have two types of geometrical isomers:
- Facial (fac): All three bidentate ligands occupy adjacent positions.
- Meridional (mer): The bidentate ligands occupy positions that are opposite each other.
Thus, (Co(Gly)3) can exhibit two geometrical isomers: fac-(Co(Gly)3) and mer-(Co(Gly)3).
Step 5: Determine Optical Activity
Optical isomers (enantiomers) are those that do not have a plane of symmetry. Since both the fac and mer isomers do not have a plane of symmetry, they can exist as optical isomers.
- For the fac isomer, it can exist in two forms (D and L).
- For the mer isomer, it can also exist in two forms (D and L).
Thus, we have a total of four optical isomers: two from the fac isomer and two from the mer isomer.
Step 6: Conclusion
The complex (Co(Gly)3) is diamagnetic (as cobalt in this oxidation state is Co(III) with no unpaired electrons), has two geometrical isomers (fac and mer), and four optical isomers (D and L forms of both geometrical isomers).
Final Answer
The diamagnetic complex which has two geometrical and four optically active isomers is (Co(Gly)3).
---
We need to identify a complex that is diamagnetic, has two geometrical isomers, and four optically active isomers. The complex mentioned in the video is (Co(Gly)3) where Glycine acts as a bidentate ligand.
Glycine (Gly) is a bidentate ligand, meaning it can coordinate to the metal center through two different donor atoms. In this case, Glycine coordinates through its nitrogen and oxygen atoms.
The complex (Co(Gly)3) has an octahedral geometry because it is a coordination complex with a central metal ion surrounded by six donor atoms (three Glycine ligands).
In an octahedral complex with bidentate ligands, we can have two types of geometrical isomers:
- Facial (fac): All three bidentate ligands occupy adjacent positions.
- Meridional (mer): The bidentate ligands occupy positions that are opposite each other.
Optical isomers (enantiomers) are those that do not have a plane of symmetry. Since both the fac and mer isomers do not have a plane of symmetry, they can exist as optical isomers.
- For the mer isomer, it can also exist in two forms (D and L).
The complex (Co(Gly)3) is diamagnetic (as cobalt in this oxidation state is Co(III) with no unpaired electrons), has two geometrical isomers (fac and mer), and four optical isomers (D and L forms of both geometrical isomers).
The diamagnetic complex which has two geometrical and four optically active isomers is (Co(Gly)3).
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - G. Organometallic Compounds, Synergic Bonding52videos
COORDINATION COMPOUNDS
- BOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - REASONING TYPE59videos
COORDINATION COMPOUNDS
- BOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - E. Stability, Colour and Magnetic Properties of Complexes60videos
COORDINATION COMPOUNDS
- BOOK - GRB PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Subjective Type63videos
CHEMICAL KINETICS
- BOOK - GRB PUBLICATIONCHAPTER - D-BLOCK ELEMENTSEXERCISE - Subjective Type18videos
D-BLOCK ELEMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
The complex which exhibits geometrical as well as optical isomerism is :
A[Co(gly)3]B[Pt(gly)2]C[Co(en)3]Cl3DK3[Co(Ox)3] - Question 2 - Select One
The complex which exhibits geometrical as well as optical isomerism is :
A[Co(gly)3]B[Pt(gly)2]C[Co(en)3]Cl3DK3[Co(Ox)3] - Question 3 - Select One
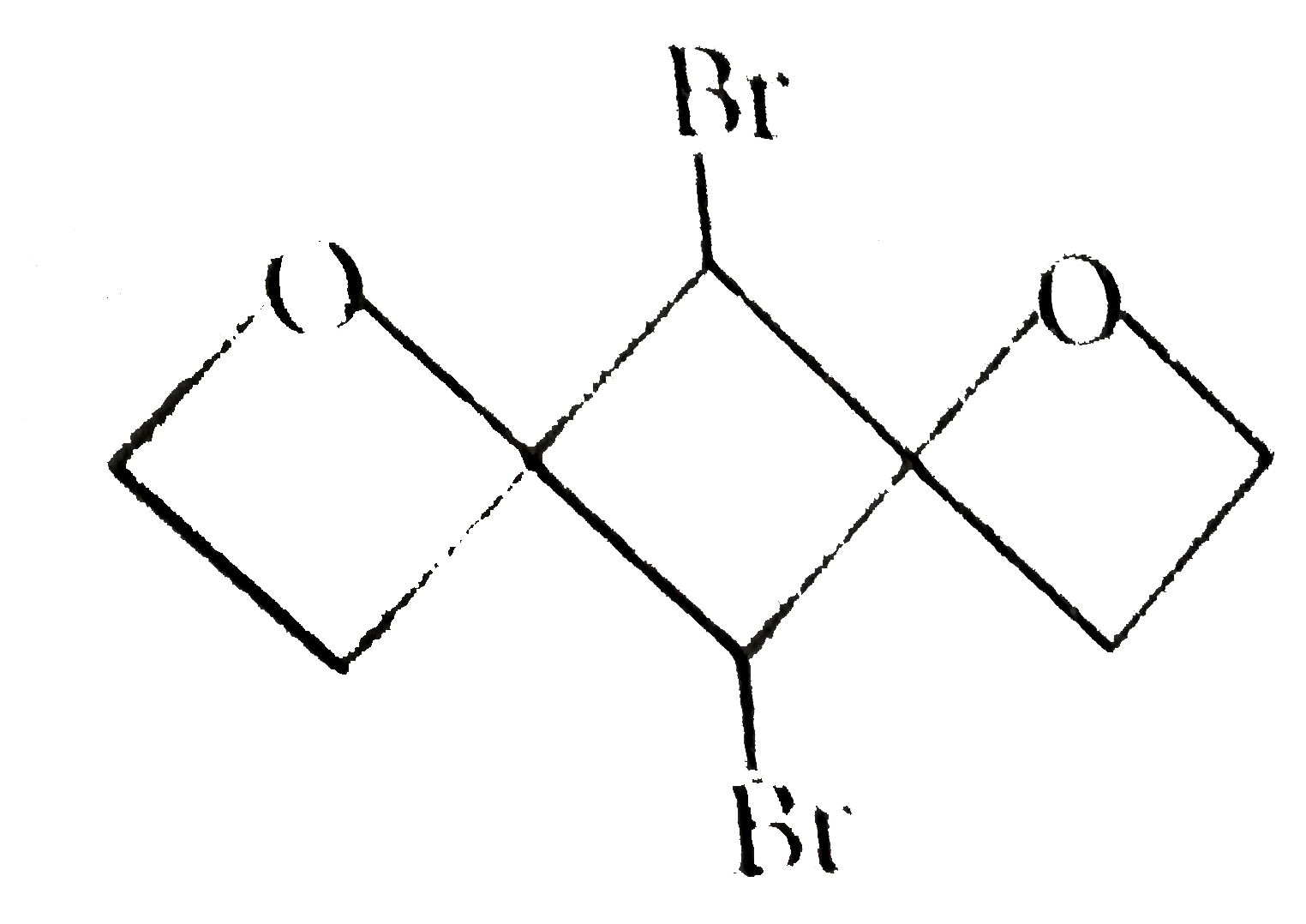 Number of optically active isomer is/are :A0B1C2D3
Number of optically active isomer is/are :A0B1C2D3
The complex entity which shows geometrical as well as optical isomerism, is :
View SolutionThe complex entity which shows geometrical as well as optical isomerism, is :
View SolutionThe optically active complex are
View SolutionThe inner orbital complex which exhibits both geometrical as well as optical isomerism.
View SolutionThe inner orbital complex which exhibits both geometrical as well as optical isomerism.
View Solution


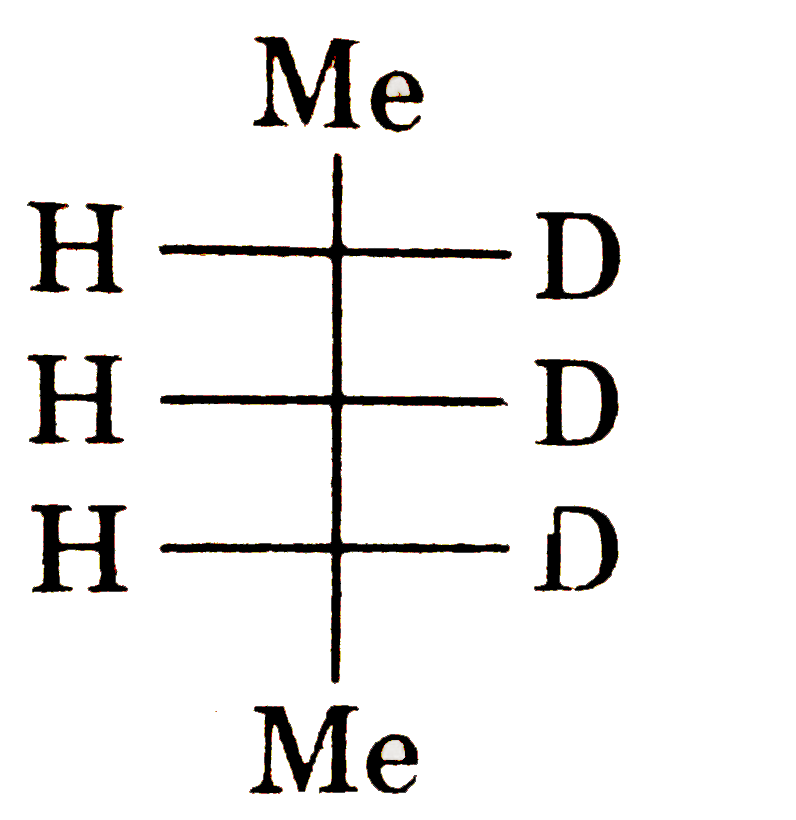
 Number of optically active isomer is/are :
Number of optically active isomer is/are :