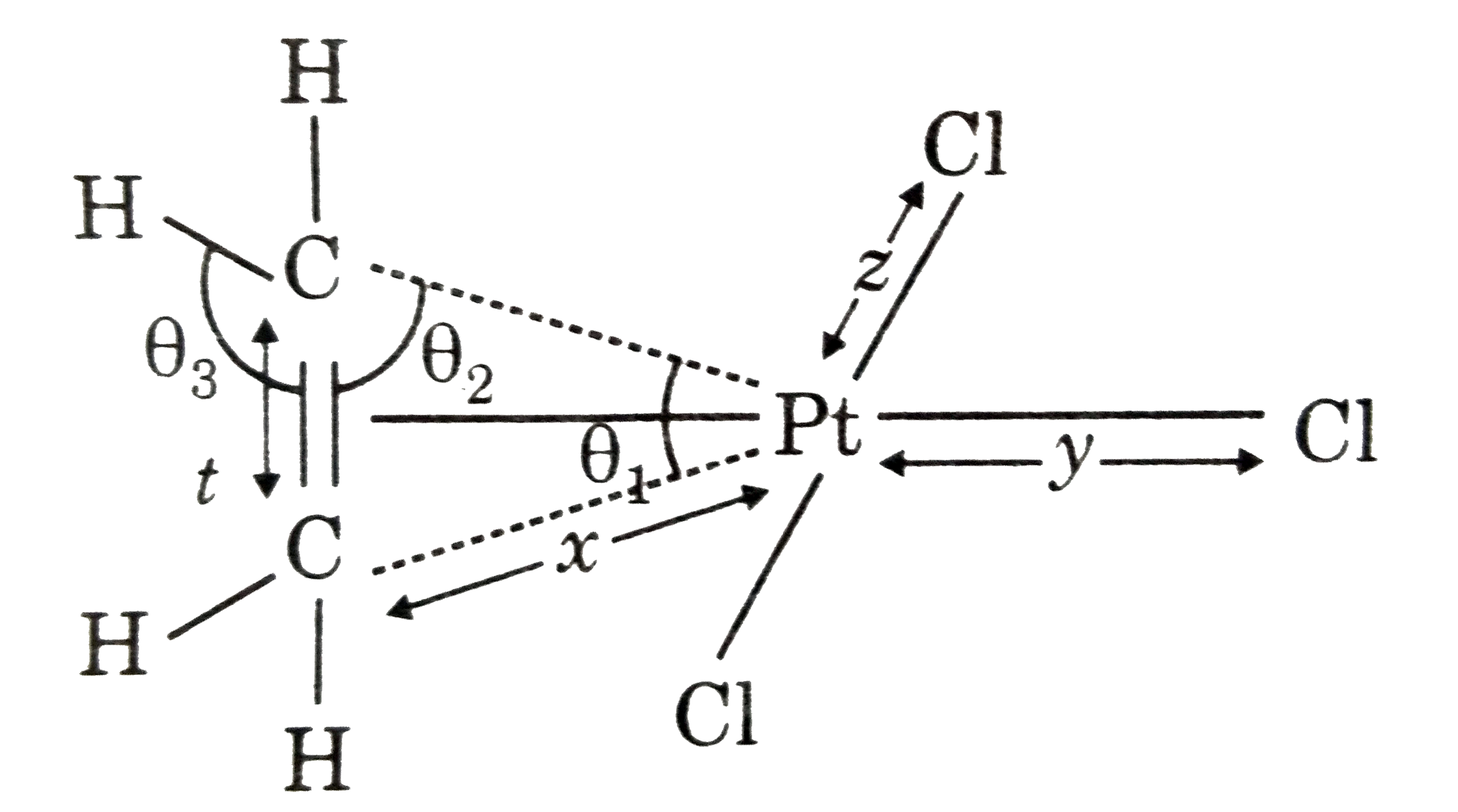
Here, θ1,θ2 and θ3 are bond angles, x, y, z, t are bond lengths in ZEISE'S Salt.
Write the number of correct relationships
(a)y<z (b)x>z
(c)x>y (d)t<y
(e)θ1<θ2 (f)θ3>θ2
(g)x=y=z (h)θ1=θ2
The correct Answer is:3
x=2.13Å,y=2.33Å,z=2.30Å,t=1.37Å,θ1=38∘,θ2=71∘,θ3=120∘
Correct relationship (d),(e ),(f)
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - MATCH THE COLUMN TYPE
41 Videos
- CHEMICAL KINETICSBOOK - GRB PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Subjective Type
63 Videos
- D-BLOCK ELEMENTSBOOK - GRB PUBLICATIONCHAPTER - D-BLOCK ELEMENTSEXERCISE - Subjective Type
18 Videos
Similar Questions
Knowledge Check
If x=θ−1θ and y=θ+1θ, then: d2ydx2=
AyxBx2−y2y3Cy2−x2x3Dy2−x2y3If x=logθ,θ>0andy=1θ,thend2ydx2=
A0B1CdydxD−(dydx)If secθ−tanθ=xy(0<x<y)and0∘<θ<90∘ , then sinθ is equal to
Ay2−x2x2+y2Bx2+y2y2−x2C2xyx2+y2Dx2+y22xy
If the acute angle between the pairs of lines 3x2−7xy+4y2=0 and 6x2−5xy+y2=0 be θ1 and θ2 respectively, then
(A) θ1=θ2
(B) θ1=2θ2
(C) 2θ1=θ2
(D) None of these
View SolutionIf the angle between the plane x−3y+2z=1 and the line x−12=y−11=z−1−3 is θ, then the value of cosecθ is
View SolutionIf 0<θ<π and the system of equations
(sinθ)x+y+z=0
x+(cosθ)y+z=0
(sinθ)x+(cosθ)y+z=0
has a non-trivial solution, then θ=
View SolutionIf 0<θ<π and the system of equations
(sinθ)x+y+z=0
x+(cosθ)y+z=0
(sinθ)x+(cosθ)y+z=0
has a non-trivial solution, then θ=
View SolutionA block X kept on an inclined surface just begins to slide if the inclination is θ1 The block is replaced by another block Y and it is found that it just begins to slide if the inclination is θ2,(θ2>θ1) Then .
View Solution
