What is the value of $6 t$ such that volume contained inside the planes $\sqrt{1 - t^{2}} x + t z = 2 \sqrt{1 - t^{2}}, z = 0, x = 2 + \frac{t \sqrt{4 t^{2} - 5 t + 2}}{\sqrt{12 {(1 - t^{2})}^{1 / 4}}}$ and $| y | = 2$ is maximum.

Text Solution

Verified by Experts

The correct Answer is:2

All the given planes are at right to $x z$ plane so a across section paallel to $z x$ plane will be same every where. So, volume will be maximum when area of triangular cross section is maximum.
When we cut these planes by the plane $y = 0$ , the triangle obtained is $A B C$ , where
$A B = \frac{t \sqrt{4 t^{2} - 5 + 2}}{\sqrt{12} {(1 - t^{2})}^{1 / 4}}$
Let $C A B = θ =$ angle between first and $x y$ plane, the $cos θ = t$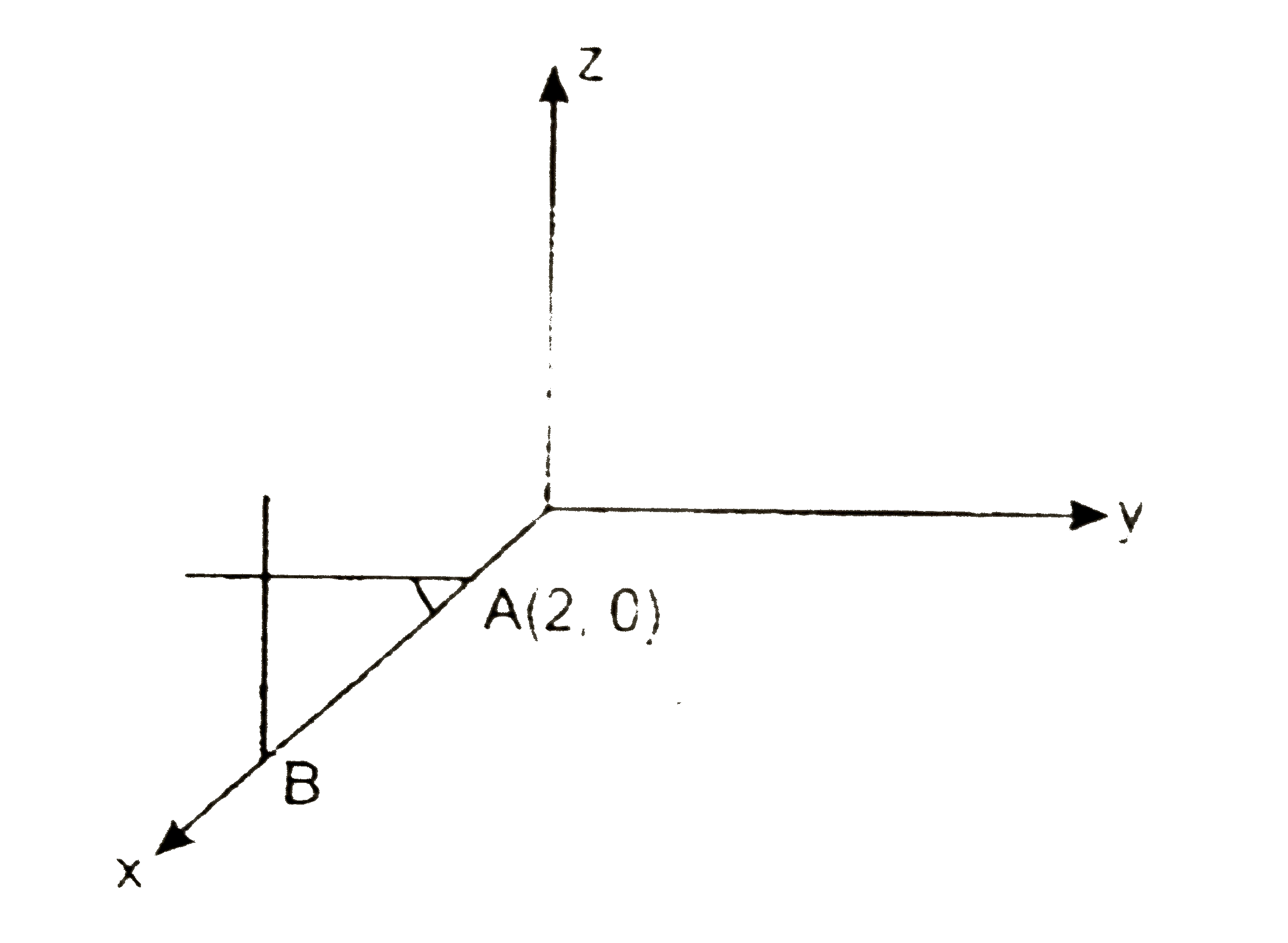
Area of $Δ A B C = Δ = \frac{1}{2} {(A B)}^{2} tan θ$
$Δ = \frac{1}{2} \frac{t^{2} (4 t^{2} - 5 t + 2)}{12 {(1 - t^{2})}^{\frac{1}{2}}} \times \frac{\sqrt{1 - t^{2}}}{t} = \frac{1}{2} \frac{4 t^{3} - 5 t^{2} + 2 t}{12}$
For example $\frac{d Δ}{d t} = 0 \Rightarrow 12 t^{2} - 10 t + 2 = 0$
$\Rightarrow t = \frac{10 \pm \sqrt{100 - 96}}{24} = \frac{1}{2}$ or $\frac{1}{3}$
Now, $\frac{d^{2} Δ}{{d t}^{2}} = 24 t - 10$
So, $Δ$ " is maximum at " $t = \frac{1}{3}$ "and minimum at " $t = \frac{1}{2}$
$∴ t = \frac{1}{3}$

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The conic having parametric representation $x = \sqrt{3} ((1 - \frac{t^{2}}{1 + t^{2}}), y \frac{= 2 t}{1 + t^{2}}$ is
Aan circle
Ba parabola
Can ellipse
Da hyperbola
If $x = \sqrt{\frac{1 - t^{2}}{1 + t^{2}}} and y = (\sqrt{1 + t^{2}} - \sqrt{1 - t^{2}})$ then the value of $\frac{d^{2} y}{{d x}^{2}}$ at t=0 is given by
A0
B $1 / 2$
C1
D $- 1$
If $cos x = \frac{1}{\sqrt{1 + t^{2}}}$ , and $sin y = \frac{t}{\sqrt{1 + t^{2}}}$ , then $\frac{d y}{d x}$ =
A $- 1$
B $\frac{1}{1 + t^{2}}$
C $\frac{1 - t}{1 + t^{2}}$
D1

RESONANCE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile