Doubtnut Promotions Sticky

If α,βγ are the roots of the equation x3+px2+qx+r=0, then (1−α2)(1−β2)(1−γ2) is equal to
(a)   (1+q)2−(p−r)2   (b)   (1+q)2+(p+r)2
(c)   (1−q)2+(p−r)2   (d)   none of these

A

(1+q)2)−(p+r)2

B

(1+q)2+(p+r)2

C

(1−q)2+(p−r)2

D

(1+r)2−(p+q)2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

x3+px2+qx+r=0 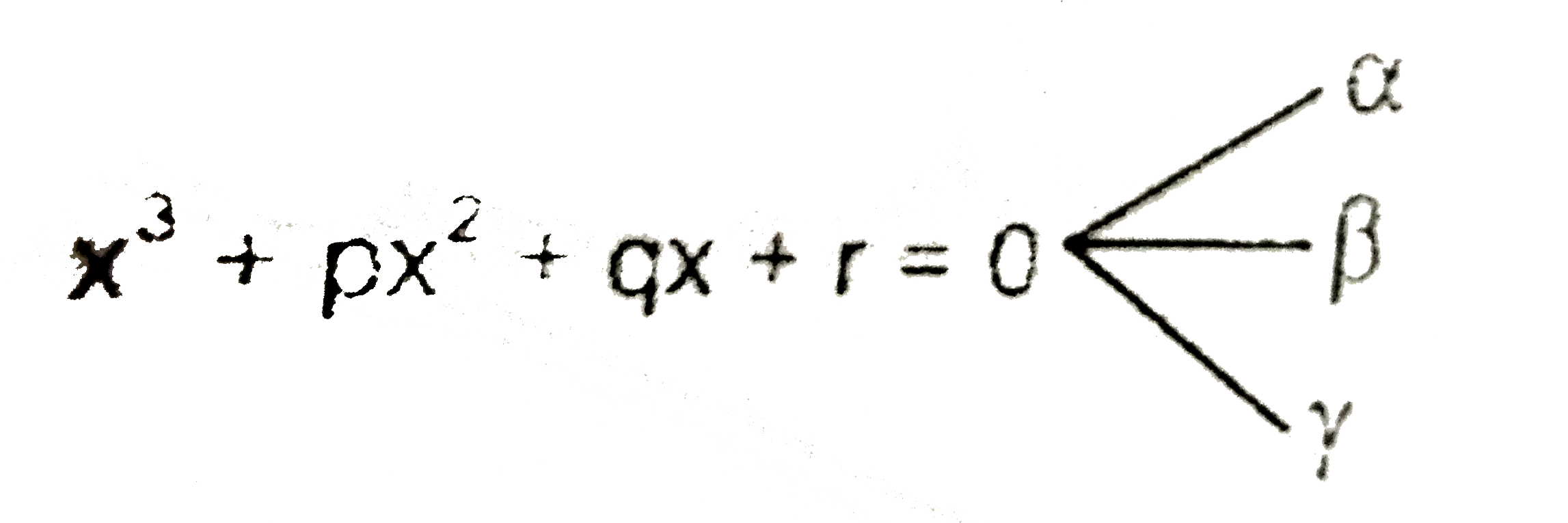ocr_image
x3+px2+qx+r=(x−α)(α−β)(x−γ)=1+p+q+r…………1
pur x=−1
⇒−(1+α)(1+β)(1+γ)=−1+p−q+r……..2
Multiplying (1) & (2)
(1−α2)(1−β2)(1−γ2))={(1+q)+(p+r))((1+q)−(p+r)}
=(1+q)2−(p+r)2

|
Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions