The area covered by the curve y=max{2−x,2,1+x} with x-axis from x=−1 to x=1 is αβ, then α−β= (where α,β are coprime to each other)
Video Solution
Text Solution
The correct Answer is:7
y=max{2−x,1+x} 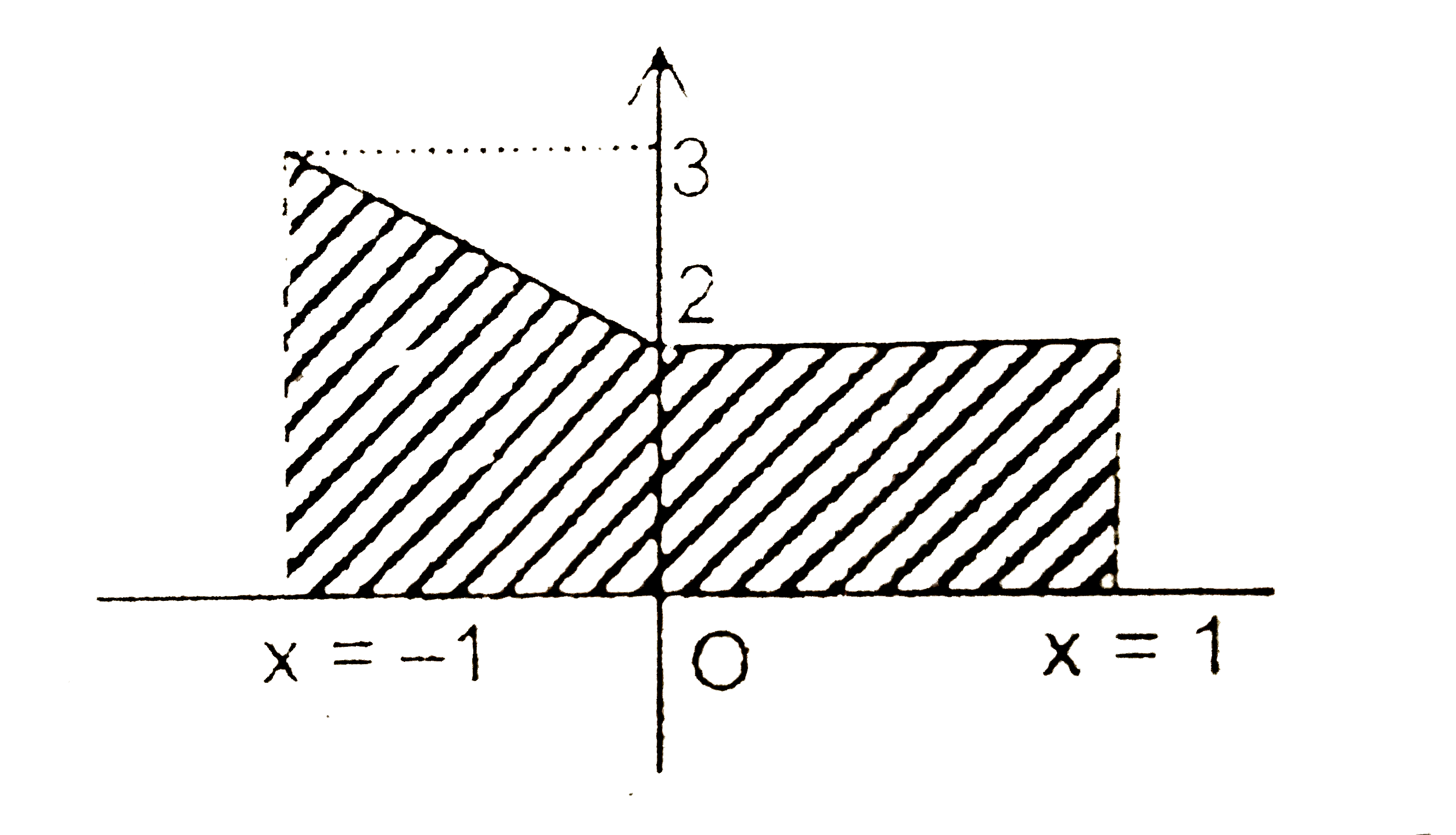
Area =(12(2+3)×1)+1×2=92=αβ∴α−β=7
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If 1∈(α,β) where α,β are the roots of the equation x2−a(x+1)+3=0, then
Aa>2Ba<−6anda>2C−6<a<2Da<2
If the equation sin−1x=cosec−1x is satisfied for α and β, (α≠β), then α+β is equal to
View SolutionIf α,β are the zeroes of the polynomials f(x)=x2−3x+6 then find the value of 1α+1β+α2+β2−2αβ
View SolutionConsider the equation x2−5x+2=0 with roots α,β, then the value of α+β+α−1+β−1=?
View SolutionIf α and β are zeroes of the polynomial 3x2−7x+1 then find the value of 1α+1β
View SolutionIf αandβ are the zeroes of the quadratic polynomial 4x2−2x+1 find α2+β2and1α+1β.
View SolutionIf α and β are the zeros of the quadratic polynomial f(x)=x2−x−4 , find the value of 1α+1β−αβ .
View SolutionIf α and β are zeros of polynomial f(x)=2x2+11x+5, then find
(i) α4+β4, (ii) 1α+1β−2αβView Solution

