Inside a solid glass sphere of radius $R$ , a point source of light lies at a distance $x (x < R)$ from centre of the sphere. The solid is surrounded by air of refractive index 1. The maximum angle of incidence for rays incident on the spherical glass air interface directly from the point soure is:

A

${cos}^{- 1} \frac{x}{R}$

B

${sin}^{- 1} \frac{x}{R}$

C

${cos}^{- 1} \sqrt{\frac{x}{R}}$

D

${sin}^{- 1} \sqrt{\frac{x}{R}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $O$ be the centre of $A$ be the point source for ray incident
at any point $P$ t angle have maxmum angle of incidence $i$ ,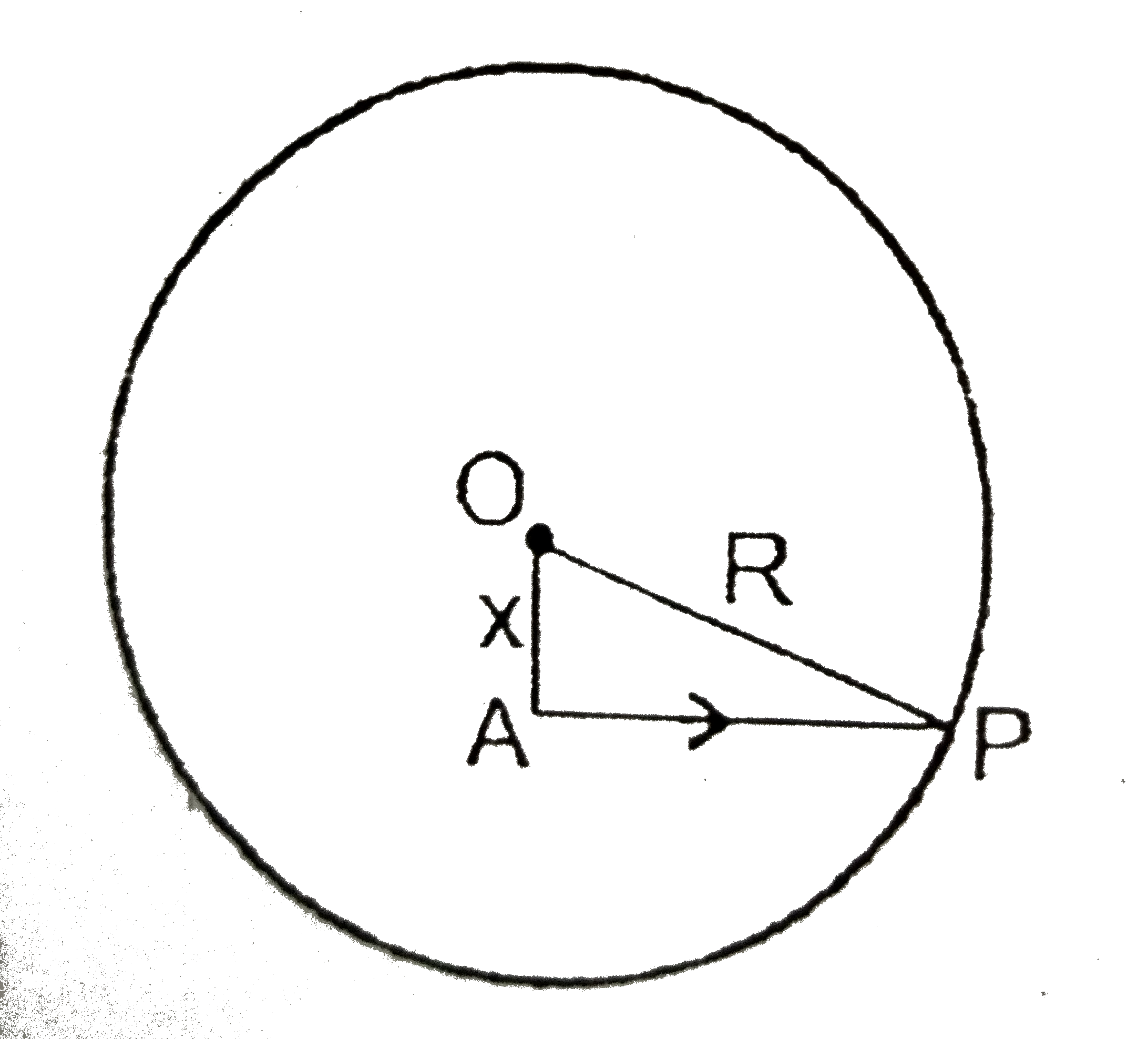

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One

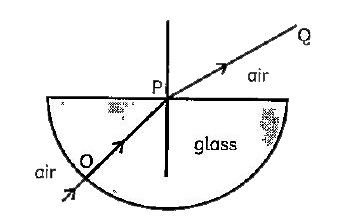
The angle of incidence from air to glass at the point O on the hemispherical glass slab is.
A $45^{\circ}$
B $0^{\circ}$
C $90^{\circ}$
D $180^{\circ}$
Question 2 - Select One
A ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
A ${tan}^{- 1} (2 / 3)$
B ${sin}^{- 1} (2 / 3)$
C $90^{\circ}$
D ${cos}^{- 1} (1 / 3)$
Question 3 - Select One
A ray of light is incident on a glass sphere of refractive index $3 / 2$ . What should be the angle of incidence so that the ray which enters the sphere does not comme out of the sphere?
A ${tan}^{- 1} (2 / 3)$
B $60^{\circ}$
C $90^{\circ}$
D $30^{\circ}$

Recommended Questions

Home
Ask Doubt
Profile