For positive integers k=1,2,3,....n,, let $S_{k}$ denotes the area of $△ A O B_{k}$ such that $∠ A O B_{k} = \frac{k π}{2 n}$ , OA=1 and $O B_{k} = k$ The value of the $lim n \to \infty \frac{1}{n^{2}} n \sum k - 1 S_{k}$ is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:0

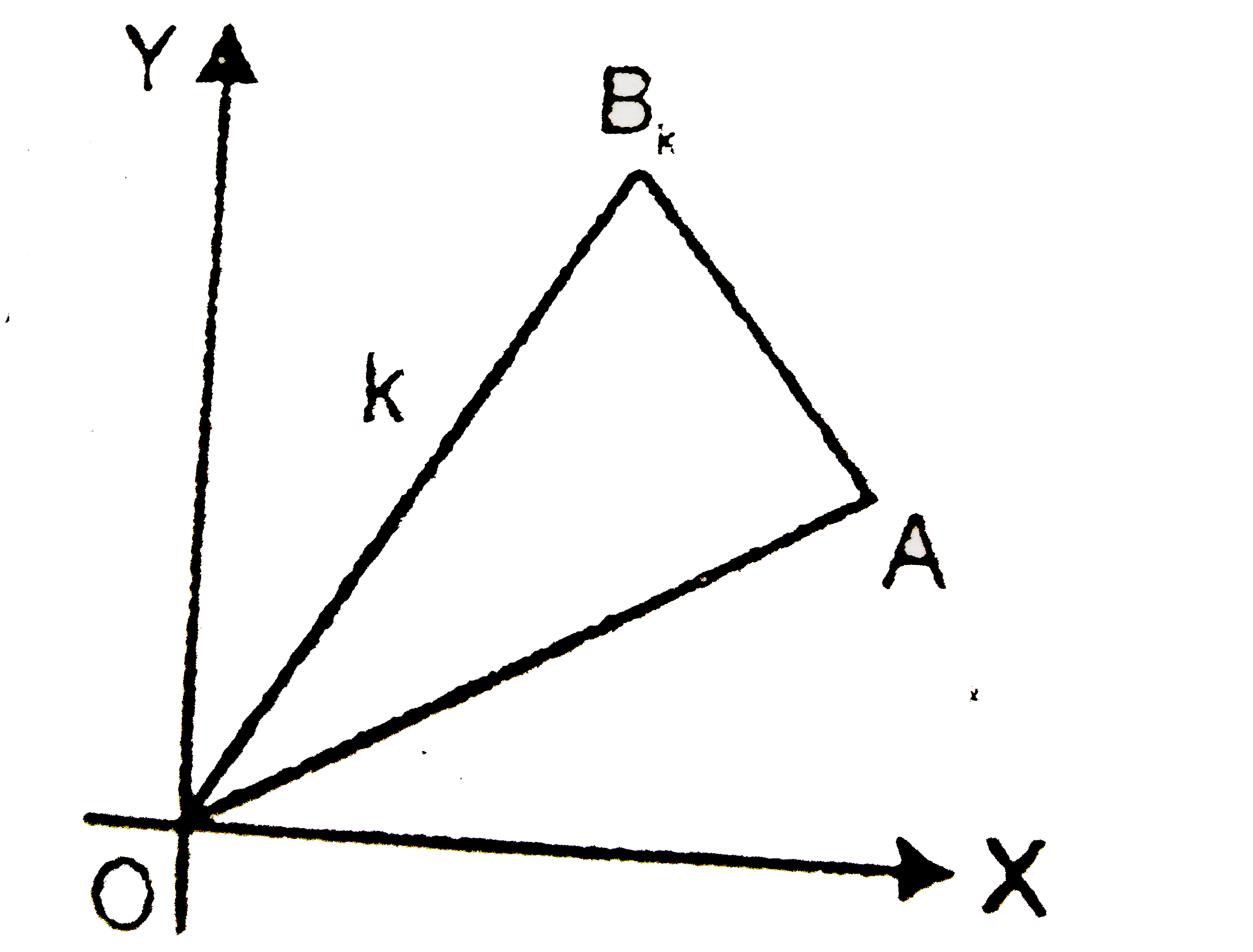
$O B_{k} = k, ∠ A O B_{k} = \frac{k π}{2 n}$
$S_{k} = \frac{1}{2} k sin \frac{k π}{2 n}$ (using $Δ = \frac{1}{2} ∣ ∣ ∣ \int ∣ ∣ ∣ h η$ )
$∴ L = lim n \to \infty \frac{1}{n^{2}} n \sum k = 1 S_{k} = \frac{k}{2 n^{2}} \infty \sum k = 1 sin \frac{k π}{2 n}$
$= \frac{1}{2 n} \infty \sum k = 1 \frac{k}{n} sin \frac{k π}{2 n} = \frac{1}{2} \int_{0}^{1} x . sin \frac{π x}{2} d x$
$= \frac{1}{2} [\frac{- 2}{π} \times cos \frac{π x}{2} ∣_{0}^{1} + \frac{2}{π} \int_{0}^{1} cos \frac{π x}{2} d x]$
$= \frac{1}{2} [0 + \frac{2}{π} \frac{.2}{π} {(sin \frac{π x}{2})}_{0}^{1}] = \frac{2}{π}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The value of $lim x \to \infty n \sum k = 1 (\frac{k}{n^{2} + n + 2 k}) =$
A $\frac{1}{4}$
B $\frac{1}{3}$
C $\frac{1}{2}$
D $1$
Question 2 - Select One
Consider a parabola $y = \frac{x^{2}}{4}$ and the point $F (0, 1) .$
Let $A_{1} (x_{1}, y_{1}), A_{1} (x_{2}, y_{2}), A_{3} (x_{3}, y_{3}), ... . ., A_{n} (x_{n}, y_{n})$ are 'n' points on the parabola such $x_{k} > - and ∠ O F A_{k} = \frac{k π}{2 π} (k = 1, 2, 3, ... ..., n) .$ Then the value of $lim n \to \infty \frac{1}{n} n \sum k = 1 F A_{k},$ is equal to :
A $\frac{2}{π}$
B $\frac{4}{π}$
C $\frac{8}{π}$
DNone of these
Question 3 - Select One
Consider a parabola $y = \frac{x^{2}}{4}$ and the point $F (0, 1) .$
Let $A_{1} (x_{1}, y_{1}), A_{1} (x_{2}, y_{2}), A_{3} (x_{3}, y_{3}), ... . ., A_{n} (x_{n}, y_{n})$ are 'n' points on the parabola such $x_{k} > - and ∠ O F A_{k} = \frac{k π}{2 π} (k = 1, 2, 3, ... ..., n) .$ Then the value of $lim n \to \infty \frac{1}{n} n \sum k = 1 F A_{k},$ is equal to :
A $\frac{2}{π}$
B $\frac{4}{π}$
C $\frac{8}{π}$
DNone of these

RESONANCE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile