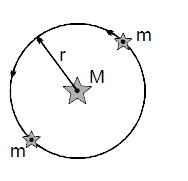
An isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M. They revolve around the central star in the same circular orbit to radius r. The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to: 
4πr3/2√G(4M+m)
2πr3/2√GM
2πr3/2√G(M+m)
4πr3/2√G(M+m)
The correct Answer is:A
Net gravitational force on any orbitin star provides necessary centripetal force.
So, GMmr2+Gm24r2=mV2r
⇒V=√G(4M+m)4r
T=2πrV=4πr3/2√G(4M+m)
Similar Questions
A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
View SolutionTwo satellites A and B are orbiting around the earth in ciruclar orbits of the same radius. The mass of A is 16 times that of B. Then the raito of the period of revolution of B to that of A is
View Solution
Knowledge Check
If a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
A4π2r3/GTB4π2r3/GT2C4π2r/GTD4π2r3/G2T2Two satellites are revolving around the earth in circular orbits of same radii. Mass of one satellite is 100 times that of the other. Then their periods of revolutions are in the ratio
A100:1B1:100C1:1D10:1_S01_034_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The orbital velocity of each star isA54√10×10/sB54√10×105m/sC54√10×102m/sD54√10×104m/s
Three identical stars of mass M form an equilateral triangle that rotates around the triangle's center as the stars move in a common circle about that center. The triangle has edge length L. What is the speed of the stars?
View Solution_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:
View Solution_S01_035_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The total machanical energy of the system is
View SolutionA satellite of mass m revolves around the earth of mass M in a circular orbit of radius r, with an angular velocity ω. If raduis of the orbit becomes 9r, then angular velocity of this orbit becomes
View SolutionA planet of mass m is moving around a star of mass M and radius R in a circular orbit of radius r. The star abruplly shrinks to half its radius without any loss of mass. What change will be there in the orbit of the planet ?
View Solution