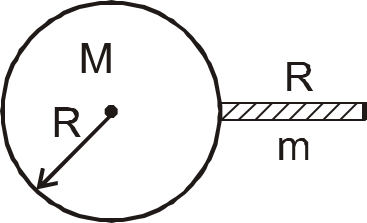
A uniform thin rod of mass $m$ and length $R$ is placed normally on surface of earth as shown. The mass of earth is $M$ and its radius $R$ . Then the magnitude of gravitational force exerted by earth on the rod is

A

$\frac{G M m}{2 R^{2}}$

B

$\frac{G M m}{4 R^{2}}$

C

$\frac{4 G M m}{9 R^{2}}$

D

$\frac{G M m}{8 R^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$F = \int_{R}^{2 R} = \frac{G M (\frac{m}{R}) d x}{x^{2}} = \frac{G M m}{2 R^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
If $M$ is the mass of the earth and $R$ its radius, the radio of the gravitational acceleration and the gravitational constant is
A $\frac{R^{2}}{M}$
B $\frac{M}{R^{2}}$
C $M R^{2}$
D $\frac{M}{R}$
Question 2 - Select One
If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
A $\frac{R^{2}}{M}$
B $\frac{M}{R^{2}}$
C $M R^{2}$
D $\frac{M}{R}$
Question 3 - Select One
A body of mass m is placed on the earth's surface . It is taken from the earth's surface to a height h = 3 R when R is the radius of the earth. The change in gravitational potential energy of the body is
A $\frac{3}{2} m g R$
B $\frac{3}{4} m g R$
C $\frac{1}{2} m g R$
D $\frac{1}{4} m g R$

Recommended Questions

Home
Ask Doubt
Profile