The ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….Solution in Telugu
sides
areas
angles
none
The correct Answer is:A
Step by step video, text & image solution for The ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding……. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SIMILAR TRIANGLES EXERCISE - OBSERVATION BITS TO SOLVE VARIOUS BITS IN THE GIVEN IN THE PUBLIC EXAMINATION29videos
SIMILAR TRIANGLES
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SETS EXERCISE - CREATIVE BITS OF CCE MODEL EXAMINATION116videos
SETS
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - STATISTICSEXERCISE - EXERCISE146videos
STATISTICS
Similar Questions
The maximum nuber of possible tangents that can be draw to a circle is ……..
05:38View SolutionLet A={1,2,{1},{1,2},3,4}, then which of the following is true?
04:03View SolutionThe mean value can be calculated from both ungrouped and grouped date . Which one you think is more accurate ? Why ?
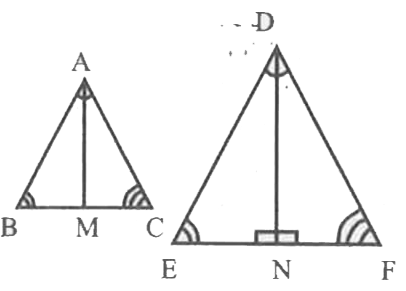
07:50View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
11:00View SolutionThe ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
05:54View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
07:55View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
05:50View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
04:35View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
 08:15View Solution
08:15View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
08:19View SolutionProve that the ratio at the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
05:15View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
03:15View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
08:01View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
06:14View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
05:57View Solution

