The magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
|B|=(μ04π)2ir
|B|=(μ04π)r2i
|B|=(4πμ0)2ir
|B|=(4πμ0)r2i
The correct Answer is:A
To find the magnetic induction (magnetic field) due to an infinitely long straight wire carrying a current i at a distance r from the wire, we can use Ampère's Law or the Biot-Savart Law. Here’s a step-by-step solution:
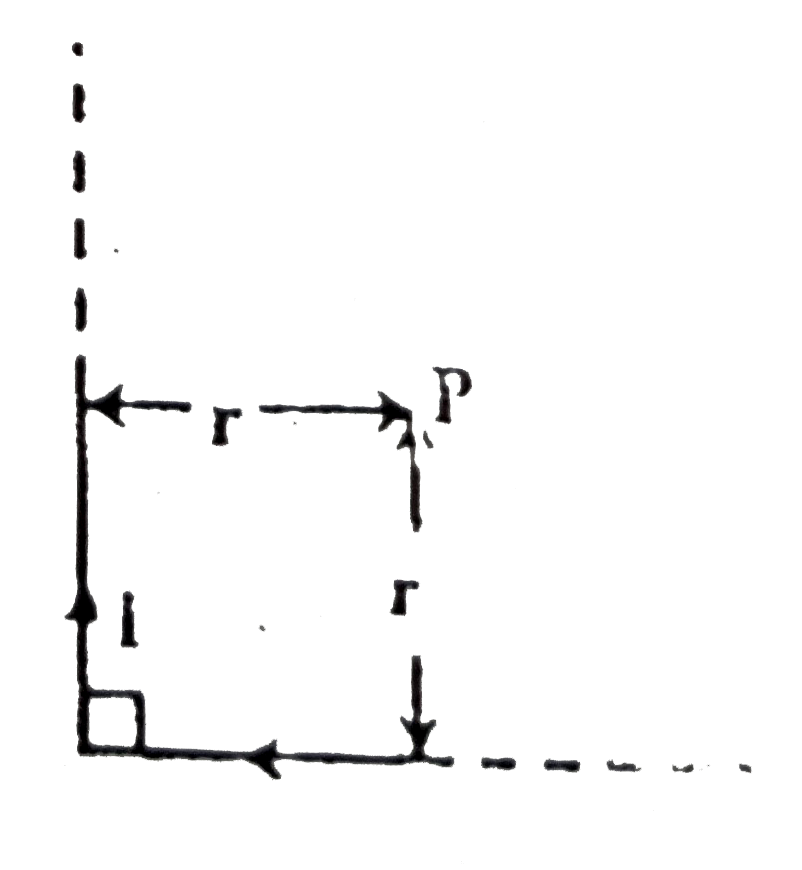
Step 1: Understanding the Configuration
We have an infinitely long straight wire carrying a current i. We want to determine the magnetic field B at a point P located at a distance r from the wire.
Hint: Visualize the wire and the point where you want to find the magnetic field.
Step 2: Using the Biot-Savart Law
The Biot-Savart Law states that the magnetic field dB at a point due to a small segment of current dl is given by:
dB=μ04πidl×^rr2
where ^r is the unit vector pointing from the current element to the point where the field is being calculated.
Hint: Remember that dl is a small length of the wire and ^r is the direction from the wire to the point P.
Step 3: Setting Up the Geometry
For an infinitely long wire, we can consider the contributions from all segments of the wire. The angle θ between dl and ^r will be important. The sine of the angle θ can be expressed in terms of the geometry of the situation.
Hint: The angle θ helps in determining how much of the current contributes to the magnetic field at point P.
Step 4: Integrating Over the Length of the Wire
Since the wire is infinitely long, we need to integrate dB over the entire length of the wire. The total magnetic field B can be calculated as:
B=∫dB=∫μ04πidlsinθr2
For an infinitely long wire, the contributions from both sides of the wire will be symmetrical.
Hint: Consider the symmetry of the problem when integrating.
Step 5: Final Expression
After performing the integration, we find that the magnetic field B at a distance r from an infinitely long straight wire carrying current i is given by:
B=μ0i2πr
Hint: This formula shows that the magnetic field decreases inversely with distance from the wire.
Conclusion
The magnetic induction (magnetic field) due to an infinitely long straight wire carrying a current i at a distance r is:
B=μ0i2πr
We have an infinitely long straight wire carrying a current i. We want to determine the magnetic field B at a point P located at a distance r from the wire.
The Biot-Savart Law states that the magnetic field dB at a point due to a small segment of current dl is given by:
dB=μ04πidl×^rr2
where ^r is the unit vector pointing from the current element to the point where the field is being calculated.
For an infinitely long wire, we can consider the contributions from all segments of the wire. The angle θ between dl and ^r will be important. The sine of the angle θ can be expressed in terms of the geometry of the situation.
Since the wire is infinitely long, we need to integrate dB over the entire length of the wire. The total magnetic field B can be calculated as:
B=∫dB=∫μ04πidlsinθr2
For an infinitely long wire, the contributions from both sides of the wire will be symmetrical.
After performing the integration, we find that the magnetic field B at a distance r from an infinitely long straight wire carrying current i is given by:
B=μ0i2πr
The magnetic induction (magnetic field) due to an infinitely long straight wire carrying a current i at a distance r is:
B=μ0i2πr
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distanceThe direction of magnetic field at a point due to an infinitely long wire carrying current is
Aparallel to the currentBantiparallel to the currentCalong the perpendicular drawn from a point on the wireDperpendicular to the plane containing the conductor and the pointA field due to a long straight wire carrying a current I is proportional to
AlBl2Cl3D√l
The field due to a long straight wire carrying a current I is proportional to
View SolutionThe strength of the magnetic field around a long straight wire, carrying current, is
View SolutionThe magnetic field lines due to a straight wire carrying a current are
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
View SolutionWhat is the magnetic induction at a distance of 5 cm from a straight wire carrying a current of 5 mA ?
View Solution
