The amplitude and maximum velocity will be respectively X=3sin2t+4cos2tThe amplitude and maximum velocity will be respectively
5,10
3,2
4,2
3,4
The correct Answer is:A
Step by step video, text & image solution for The amplitude and maximum velocity will be respectively X= 3 sin 2t + 4 cos 2tThe amplitude and maximum velocity will be respectively by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Acceleration of simple Harmonic motion
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Energy of simple Harmonic motion
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- SURFACE TENSIONBOOK - ERRORLESS CHAPTER - SURFACE TENSIONEXERCISE - Exercise
214 Videos
Similar Questions
If the maximum and minimum value of sinsinx is a and b respectively and the maximum and minimum value of coscosx is c and d respectively then a2+b2+c2+d2: (A) 1+a2 (B) 2+a2 (C) 3+a2 (D) 4+a2
View SolutionA particle is executing S.H.M. with amplitude 'A' and maximum velocity Vm. The displacement at which its velocity is half of the maximum velocity is
View Solution
Knowledge Check
If S=9t−3t3, then maximum velocity is
A0B−9 units / secC9 units/ SecD10 units /secA SHO has amplitude A and time period T. The maximum velocity will be
A4ATB2ATC2π√A/TD2πA/TFor a particle in SHM the amplitude and maximum velocity are A and V respectively. Then its maximum acceleration is
AV22ABV2ACV2ADVA
In a plane progressive wave given by y=25cos(2πt−πx), the amplitude and frequency are respectively
View SolutionIf S=16+64t−t3, then maximum velocity is
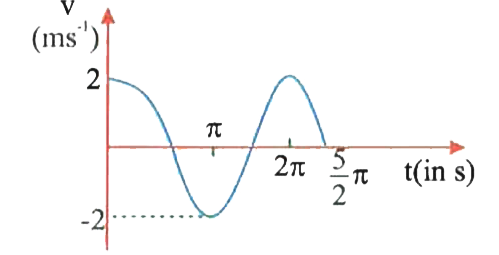
View SolutionThe velocity-time graph of a particle executing SHM is as shown in the figure. The amplitude and maximum acceleration of the particle respectively are
View SolutionEquation of displacement of a harmonic oscillator is x=15sin20πt, amplitude and angular velocity are respectively
View SolutionThe displacement ξ in centimetres of a particle is ξ=3sin314t+4cos314t. Amplitude and initial phase are
View Solution
