A spring executes SHM with mass of 10 kg attached to it. The force constant of spring is 10 N/m. If at any instant its velocity is 40 cm/sec, the displacement will be (where amplitude is 0.5 m )
0.9m
0.3m
0.03 m
0.9 m
The correct Answer is:B
To solve the problem, we will use the relationship between velocity, displacement, and angular frequency in simple harmonic motion (SHM).
1. Identify the given values:
- Mass (m) = 10 kg (not directly needed for this calculation)
- Spring constant (k) = 10 N/m
- Velocity (v) = 40 cm/s = 0.4 m/s (conversion from cm to m)
- Amplitude (A) = 0.5 m
2. Calculate the angular frequency (ω):
- The formula for angular frequency in SHM is given by:
ω=√km
- Substituting the values:
ω=√10N/m10kg=√1=1rad/s
3. Use the relationship between velocity, amplitude, and displacement:
- The relationship is given by:
v2=ω2A2−ω2x2
- Rearranging this gives:
x2=A2−v2ω2
4. Substituting the known values into the equation:
- First, calculate A2:
A2=(0.5m)2=0.25m2
- Now calculate v2:
v2=(0.4m/s)2=0.16m2/s2
- Substitute A, v, and ω into the equation:
x2=0.25−0.1612=0.25−0.16=0.09
5. Calculate the displacement (x):
- Taking the square root gives:
x=√0.09=0.3m
Final Answer:
The displacement of the mass at that instant is 0.3 m.
---
- Mass (m) = 10 kg (not directly needed for this calculation)
- Spring constant (k) = 10 N/m
- Velocity (v) = 40 cm/s = 0.4 m/s (conversion from cm to m)
- Amplitude (A) = 0.5 m
- The formula for angular frequency in SHM is given by:
ω=√km
- Substituting the values:
ω=√10N/m10kg=√1=1rad/s
- The relationship is given by:
v2=ω2A2−ω2x2
- Rearranging this gives:
x2=A2−v2ω2
- First, calculate A2:
A2=(0.5m)2=0.25m2
- Now calculate v2:
v2=(0.4m/s)2=0.16m2/s2
- Substitute A, v, and ω into the equation:
x2=0.25−0.1612=0.25−0.16=0.09
- Taking the square root gives:
x=√0.09=0.3m
The displacement of the mass at that instant is 0.3 m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:Superposition of S.H. M and Resonance
Explore 14 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:Graphical Questions
Explore 16 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:simple pendulum
Explore 61 Videos
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on motion of connected mass)
Explore 10 Videos
- SURFACE TENSIONBook:ERRORLESS Chapter:SURFACE TENSIONExercise:Exercise
Explore 214 Videos
Similar Questions
Force constant of a spring is 100 N/m. If a 10kg block attached with the spring is at rest, then find extension in the spring.
(g=10m/s2)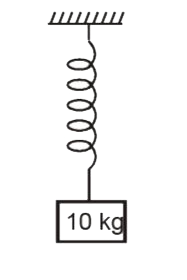
View SolutionA block of mass 4 kg while at rest is attached to an unstretched spring. The force constant of spring is 24Nm−1. If a constant horizontal force of 10 N is applied on the block, the spring gets compressed by 0.5m. What is the speed of the block at this point?
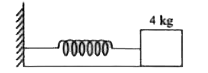
View Solution
Knowledge Check
A spring executes SHM with mass off 10 kg attached to it. The force constant of spring is 10N/m. If at any instant its velocity is 40cm/s , the displacement will be (where amplitude is 0.5m)
A0.09 mB0.3 mC0.03 mD0.9 mWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
Akl2B2 klC12MglDMglWhen a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/m
Two blocks are connected by a spring of natural length 2m.The force constant of spring is 200N/m .Find spring force in following siturations.
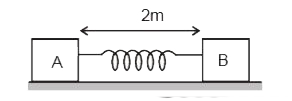
If block 'A' and 'B' both are displaced by 0.5 m in opposite direction
View SolutionA particle is executing SHM with amplitude 4 cm and has a maximum velocity of 10 cm/sec
What is its velocity at displacement 4 cm/sec ?
View SolutionA mass M attached to a spring of spring constant 0.7 N/m oscillates on a smooth horizontal table. When displacement is 0.3 m, velocity is 2 ms−1. And when displacement is 0.4 m, velocity is 0.3 m/s. Calculate the vlaue of M.
View SolutionA particle is executing SHM with amplitude 4 cm and has a maximum velocity of 10 cm/sec
What is its velocity at displacement 2 cm?
View SolutionA 2.0 - kg block executes SHM while attached to a horizontal spring of spring constant 200N/m. The maximum speed of the block as it slides on a horizontal frictionless surface is 3.0m/s.
What is the amplitude of the block's motion?
View Solution