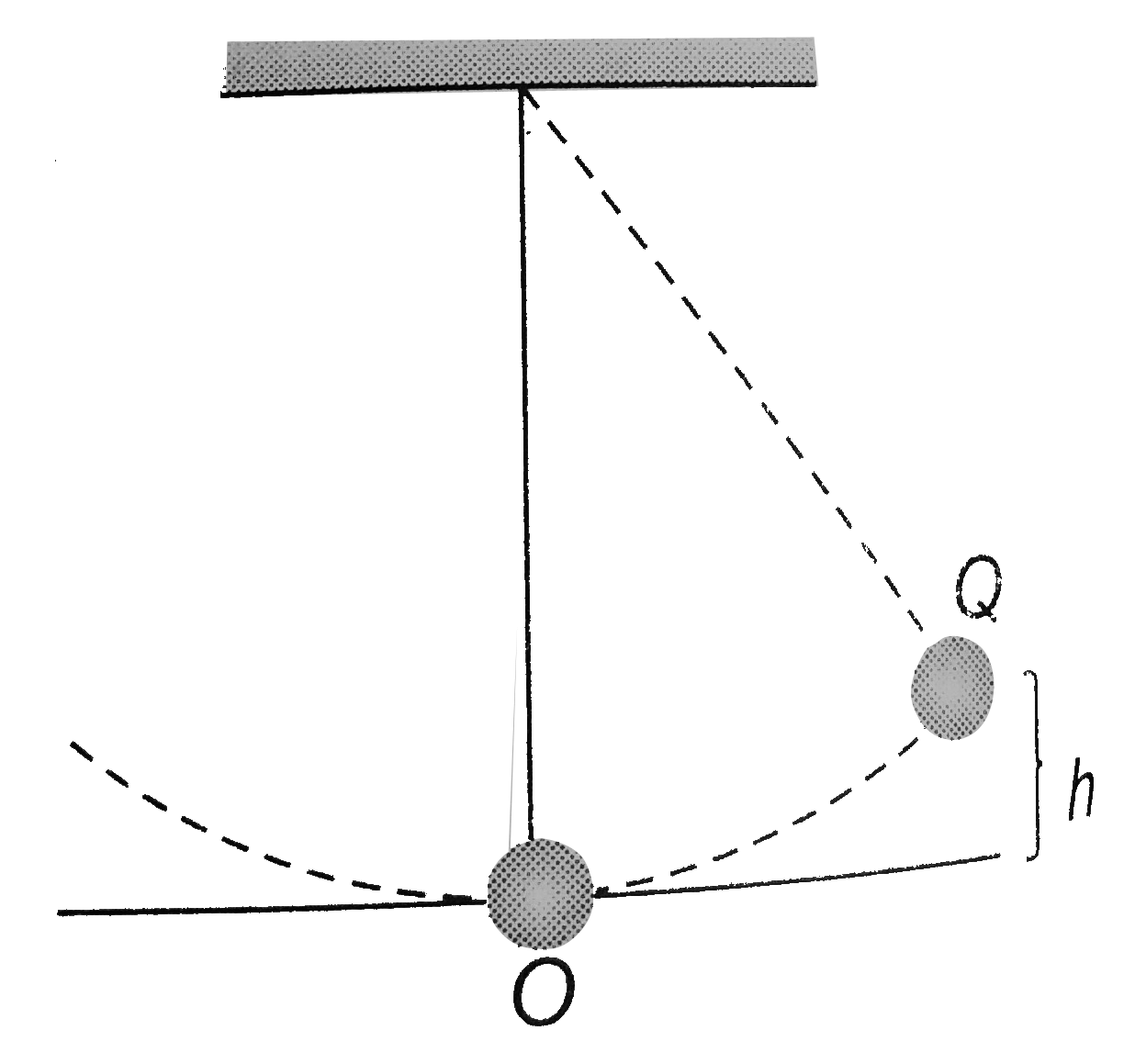
The bob of a simple pendulum it displaced position O to a equilibrium position Q which is at height h above O and the bob to then mass released Assuming the mass of the bob is m and time period 2.0 sec of oscillation to be string when the bob passes through O is
m(g=π√2gh)
m(g=√π2gh)
m(g+√π22gh)
m(g+√π23gh)
The correct Answer is:A
Step by step video, text & image solution for The bob of a simple pendulum it displaced position O to a equilibrium position Q which is at height h above O and the bob to then mass released Assuming the mass of the bob is m and time period 2.0 sec of oscillation to be string when the bob passes through O is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The bob of pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. Find the speed v with which the bob passes through the equilibrium position.
View SolutionThe bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View Solution
Knowledge Check
The bob of a simple pendulum it displaced position O to a equilibrium position Q which is at height it above O and the bob to then mass released Assuming the mass of the bob to be m and 2.0 sec of oscillation to be string when the bob passes through O is
 Am(g+π√2gh)Bm(g+π√π2gh)Cm(g+√π22gh)Dm(g+√π23gh
Am(g+π√2gh)Bm(g+π√π2gh)Cm(g+√π22gh)Dm(g+√π23ghThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
Am(g+2π2h)Bm(g+π2h)Cm(g+π22h)Dm(g+π23h)The bob of simple pendulum having length 1, is displaced from mean position to an angular position o with respect to vertical. If it is released, then velocity of bob at equilibrium position is
A√2g(1−cosθ)B√2g(1+cosθ)C√2glcosθD√2gl
A simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that height of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
View SolutionThe periodic time of a simple pendulum is 3 sec. The mass of its hollow spherical bob is 100 gram. The bob is then filled with sand, so that the mass of the bob becomes 200 gram. Then the new period of oscillation of the simple pendulum wil be
View SolutionThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
View SolutionThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
View SolutionWhat is the effect on the time period of a simple pendulum if the mass off the bob is doubled?
View Solution
