An electron is moving in electron field and magnetic field it will gain energy from
Electric field
Magnetic field
Both of these
None of these
The correct Answer is:A
To determine in which field an electron will gain energy while moving, we need to analyze the effects of both electric and magnetic fields on the electron.
1. Understanding the Electric Field:
- When an electron (which has a charge of -e) moves in an electric field (E), it experiences an electrostatic force given by:
FE=Q⋅E=−e⋅E
- The negative sign indicates that the force acts in the opposite direction to the electric field.
2. Acceleration of the Electron:
- The acceleration (a) of the electron can be calculated using Newton's second law:
a=FEme=−e⋅Eme
- Since the force is in the same direction as the velocity of the electron (due to the negative charge), the electron will accelerate in the direction of the electric field.
3. Change in Velocity:
- The velocity of the electron will increase as it accelerates:
V′=V0+a⋅t
- This increase in velocity indicates that the kinetic energy of the electron will also increase.
4. Kinetic Energy in Electric Field:
- The kinetic energy (KE) of the electron is given by:
KE=12meV2
- As the velocity increases, the kinetic energy will also increase.
5. Understanding the Magnetic Field:
- When the electron moves in a magnetic field (B), it experiences a magnetic force given by:
FB=Q⋅(V×B)=−e⋅(V×B)
- The direction of this force is always perpendicular to both the velocity of the electron and the magnetic field.
6. Effect of Magnetic Force:
- Since the magnetic force is always perpendicular to the velocity, it does not do work on the electron. Therefore, the speed (and thus the kinetic energy) of the electron remains constant:
KE=12meV2(constant)
7. Conclusion:
- In the electric field, the electron gains energy due to the work done by the electric force, leading to an increase in kinetic energy.
- In the magnetic field, the electron does not gain energy because the magnetic force does not change its speed.
Final Answer:
The electron will gain energy from the electric field.
---
- When an electron (which has a charge of -e) moves in an electric field (E), it experiences an electrostatic force given by:
FE=Q⋅E=−e⋅E
- The negative sign indicates that the force acts in the opposite direction to the electric field.
- The acceleration (a) of the electron can be calculated using Newton's second law:
a=FEme=−e⋅Eme
- Since the force is in the same direction as the velocity of the electron (due to the negative charge), the electron will accelerate in the direction of the electric field.
- The velocity of the electron will increase as it accelerates:
V′=V0+a⋅t
- This increase in velocity indicates that the kinetic energy of the electron will also increase.
- The kinetic energy (KE) of the electron is given by:
KE=12meV2
- As the velocity increases, the kinetic energy will also increase.
- When the electron moves in a magnetic field (B), it experiences a magnetic force given by:
FB=Q⋅(V×B)=−e⋅(V×B)
- The direction of this force is always perpendicular to both the velocity of the electron and the magnetic field.
- Since the magnetic force is always perpendicular to the velocity, it does not do work on the electron. Therefore, the speed (and thus the kinetic energy) of the electron remains constant:
KE=12meV2(constant)
- In the electric field, the electron gains energy due to the work done by the electric force, leading to an increase in kinetic energy.
- In the magnetic field, the electron does not gain energy because the magnetic force does not change its speed.
The electron will gain energy from the electric field.
Topper's Solved these Questions
- ELECTRON, PHOTON, PHOTOELECTRIC EFFECT AND X-RAYSBOOK - ERRORLESS CHAPTER - ELECTRON, PHOTON, PHOTOELECTRIC EFFECT AND X-RAYSEXERCISE - Cathode Rays and Positive Rays
11 Videos
- ELECTRON, PHOTON, PHOTOELECTRIC EFFECT AND X-RAYSBOOK - ERRORLESS CHAPTER - ELECTRON, PHOTON, PHOTOELECTRIC EFFECT AND X-RAYSEXERCISE - Photon and Photoelectric Effect
4 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - SET
20 Videos
- ELECTRONICSBOOK - ERRORLESS CHAPTER - ELECTRONICSEXERCISE - Selv Evaluation Test
23 Videos
Similar Questions
An electron is orbiting is a circular orbit of radius r under the influence of a constant magnetic field of strength B. Assuming that Bohr postulate regarding the quantisation of angular momentum holds good for this elerctron, find
(a) the allowed values of te radius r of the orbit.
(b) the kinetic energy of the electron in orbit
(c ) the potential energy of insteraction between the magnetic moment of the orbital current due to the electron moving in its orbit and the magnetic field B.
(d) the total energy of the allowed energy levels.
(e) the total magnetic flux due to the magnetic field B passing through the nth orbit. (Assume that the charge on the electronis -e and the mass of the electron is m).
View SolutionA protom (or an electron) is moving in a uniform magnetic field. What is the path of the proton (or an electron) if it enters (i) parallel to the field, (ii) perpendicular to the field, and (iii) at an angle to the field?
View Solution
Knowledge Check
Figure shows four situations in which an electron is moving in electric / magnetic field . In which case the de Broglie wavelength of electron is increasing ?
A B
B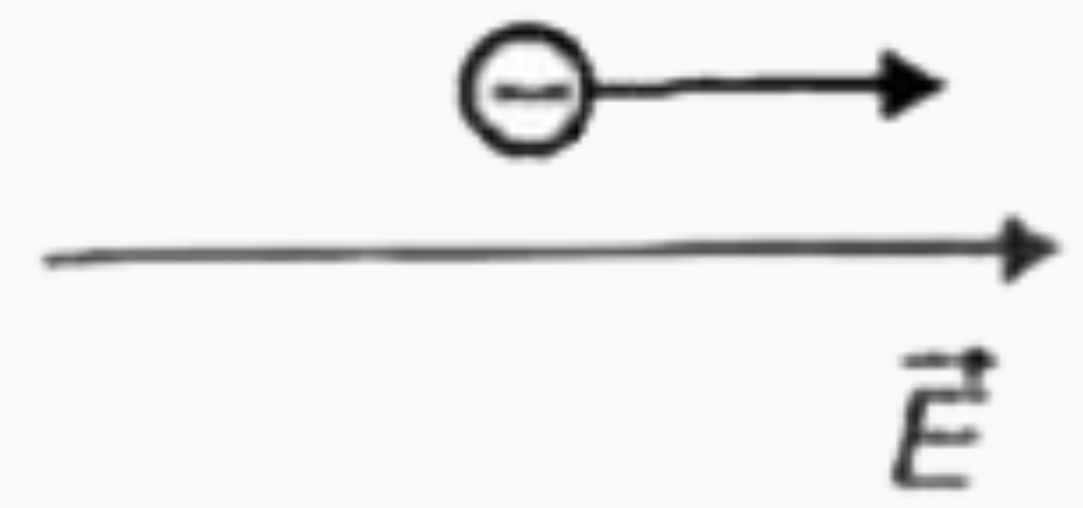 C
C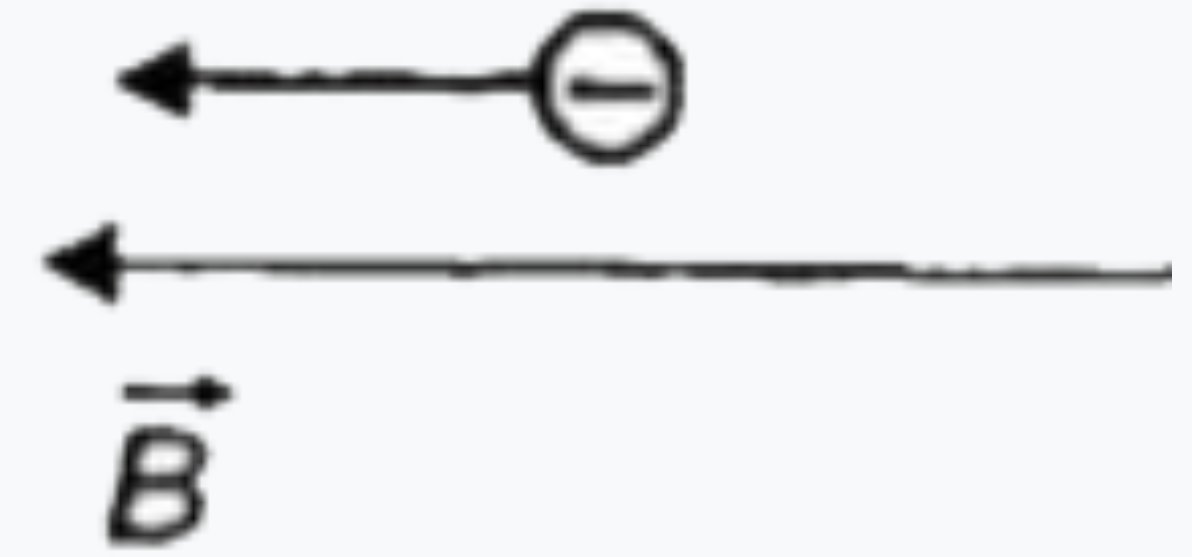 D
D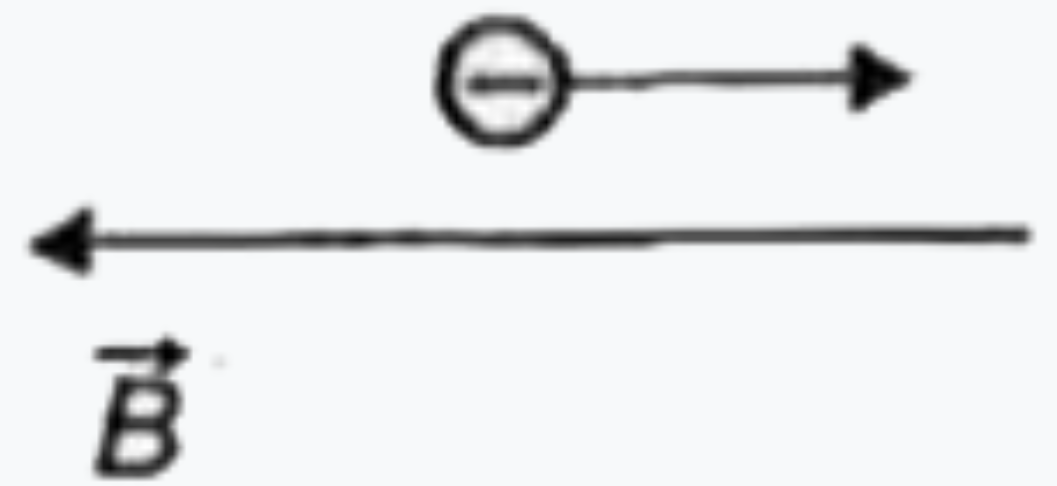
If an electron is moving with velocity v produces a magnetic field →B, then
Athe direction of field →B will be same as the direction of velocity →v.Bthe direction of field →B will be opposite to the direction of velocity →v.Cthe direction of field →B will be perpendicular to the direction of velocity →v.Dthe direction of field →B does not depend upon the direction of velocity →v.If an electron is going in the direction of magnetic field →B with the velocity of →v then the force on electron is
AZeroBe(→v.→B)Ce(→v×→B)DNone of these
The acceleration of any electron due to the magnetic fields is
View Solutionwhen an electron moves through a magnetic field , its speed will
View SolutionRadius of an electron moving in a circle in constant magnetic field is two times that of an α particle in the same field. Then de-Broglie wavelength of electrons is x-times of the α-particle Here x is
View SolutionAn electron moving towards the east enters a magnetic field directed towards the north. The force on the electron will be directed
View SolutionAccording to Biot-Savart's law, an electron moving with velocity produces a magnetic field B such that:
View Solution
